Законы подобия и обезразмеривание.
На примере рассмотренной выше задачи покажем очень важный и полезный прием, популярный в физическом моделировании, называемый обезразмериванием. При решении задач мы пользуемся системой единиц (СИ), в которой далеко не все числовые значения находятся в удобном диапазоне. Кроме того, абсолютные значения величин дают мало информации для качественного понимания. Скорость 15 м/с – это много или мало? Все дело - по сравнению с чем.
Идея обезразмеривания заключается в переходе от абсолютных значений – расстояний, скоростей, времен (s, 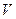 , t) и т.д. – к относительным, причем отношения строятся к величинам типичным для данной ситуации. В рассматриваемой задаче это хорошо просматривается. В задаче без сопротивления воздуха мы имеем значения l, h,
, t) и т.д. – к относительным, причем отношения строятся к величинам типичным для данной ситуации. В рассматриваемой задаче это хорошо просматривается. В задаче без сопротивления воздуха мы имеем значения l, h, 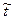 , полученные по формулам (2)-(4). Сопротивление воздуха изменит характер движения. Возьмем значения l, h,
, полученные по формулам (2)-(4). Сопротивление воздуха изменит характер движения. Возьмем значения l, h, 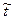 в качестве типичных для данной задачи и введем в качестве переменных величины
в качестве типичных для данной задачи и введем в качестве переменных величины
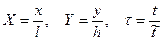 .
.
X, Y, 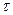 – это безразмерные расстояния по осям и безразмерное время. Тогда при отсутствии сопротивления воздуха они будут изменяться в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления.
– это безразмерные расстояния по осям и безразмерное время. Тогда при отсутствии сопротивления воздуха они будут изменяться в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления.
Введем безразмерные переменные для скоростей. Их естественно ввести, соотнося проекции скорости на оси х и у с начальной скоростью 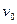 :
:
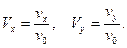
Теперь к безразмерным переменным нужно перейти в уравнениях систем (9)-(10).
Покажем, как перейти к безразмерным переменным в уравнениях системы (9) на примере второго уравнения этой системы.
Имеем:
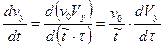 ,
,
так как постоянный множитель можно вынести за знак производной.
Подставляя это в уравнение (9), получаем:
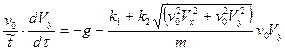
или

Подставляя 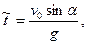 получаем:
получаем:
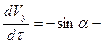 a
a 
где a, b -- безразмерные комбинации параметров, входящих в исходные уравнения,
a 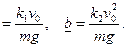
Аналогично выполним обезразмеривание во всех уравнениях систем (9), (10) и получим:

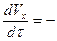 a
a 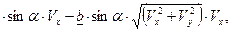
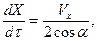 (11)
(11)
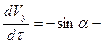 a
a 

Начальные условия для безразмерных переменных имеют вид:
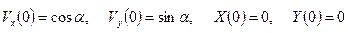
Важнейшая роль обезразмеривания – установление законов подобия. У изучаемого движения есть множество вариантов, определяемых наборами значений параметров, входящих в систему уравнений (9) -- (10) и являющихся для них начальными условиями: 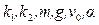 . После обезразмеривания переменных появляются безразмерные комбинации параметров a, b. В данном случае a, b, α – фактически определяют характер движения.
. После обезразмеривания переменных появляются безразмерные комбинации параметров a, b. В данном случае a, b, α – фактически определяют характер движения.
Закон подобия: Если мы изучаем два разных движения с разными размерными параметрами, но такие, что a, b, α – одинаковые, тогда движения будут качественно одинаковыми.
Число таких комбинаций обычно меньше числа размерных параметров (в данном случае вдвое), что также создает удобства при полном численном исследовании задачи. Наконец, как уже отмечалось, величины 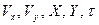 физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден.
физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден.
Прежде чем предпринимать численное моделирование, отметим, что при учете лишь линейной составляющей силы сопротивления модель допускает аналитическое решение.
Исследование задачи при произвольных значениях a, b, α будет выполняться на практике с помощью программы на языке Turbo Pascal.
Дата добавления: 2015-01-13; просмотров: 7534;
