МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕПЛОПРОВОДНОСТИ
Процесс теплопроводности – один из, так называемых, процессов тепломассопереноса, играющих огромную роль в природе и в технике. Другие процессы такого рода – диффузия, благодаря которой смешиваются разные жидкости или газы, процессы гидродинамики и аэродинамики (переноса жидкостей и газов).
Хотя каждый из таких процессов имеет собственные закономерности, между ними много общего:
1) эти процессы происходят в сплошной среде;
2) при их математическом моделировании используется один и тот же математический аппарат – дифференциальные уравнения в частных производных.
Понятие «сплошная среда» широко используется в науке. Во многих ситуациях жидкости, газы, твердые тела можно рассматривать как «сплошные», отвлекаясь от их молекулярного и атомарного устройства. Например, при изучении процессов распространения тепла или диффузии можно отвлечься от атомарного строения вещества и оперировать такими характеристиками как теплоемкость, теплопроводность, скорость диффузии и др., которые можно исследовать и практически использовать без выяснения их микроскопической природы.
В приближении сплошной среды свойства объекта описываются математически с помощью непрерывных функций координат и времени: f(x,y,z,t). За каждым свойством закрепляется своя функция, связь между ними дает полное описание среды.
Существующие задачи можно разделить на два класса: статические и динамические. В первом случае значения величин, характеризующих сплошную среду, не зависят от времени – f(x,y,z). Требуется найти их пространственное распределение – поле распределения. Во втором случае f(x,y,z,t) и нужно дать описание полей распределения во времени. Например, исследовать изменение температуры в разных точках тела, которое подогревается от источников тепла, интенсивность которых меняется со временем.
Ограничимся одной из самых простых задач данного класса – переносом тепла в однородном стержне. Рассмотрим линейный стержень, боковая поверхность которого не проводит тепла (теплоизолирована). Если в начальный момент стержень неравномерно нагрет, то в нем будет происходить перераспределение тепла. При отсутствии внутренних источников тепла его температура, в конце концов, выровняется.
Поскольку стержень линеен и однороден, то распределение температуры в пространстве характеризуется одной координатой х.
Температура (обозначим ее u) зависит от х; кроме того, она может меняться со временем, т.е. является функцией двух переменных u(x, t). Изменение этой функции вдоль стержня определяется производной по х, а изменение ее со временем определяется производной по t. Они взаимосвязаны и входят в одно уравнение.
Уравнение теплопроводности.Выведем уравнение, описывающее процесс изменения температуры в стержне. Зафиксируем некоторую точку х0 и выделим около нее малый участок стержня длиной 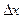 .
.
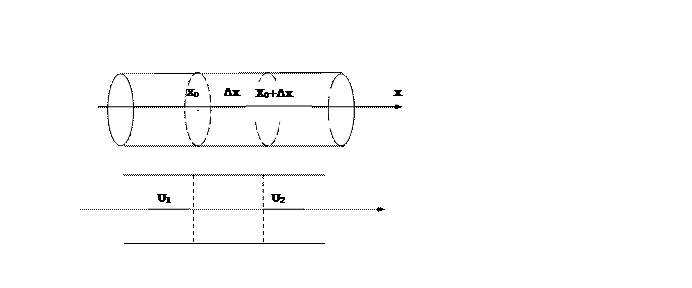 Искомое уравнение есть уравнение теплового баланса, т.е. изменение количества тепла в избранном участке стержня за счет притока и (или) оттока его через два сечения приведет к нагреванию или охлаждению этого участка в соответствии с его теплоемкостью. Выразим все это математическим языком.
Искомое уравнение есть уравнение теплового баланса, т.е. изменение количества тепла в избранном участке стержня за счет притока и (или) оттока его через два сечения приведет к нагреванию или охлаждению этого участка в соответствии с его теплоемкостью. Выразим все это математическим языком.
Количество тепла, проходящее через поперечное сечение стержня в точке х0 за время 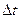 , пропорционально площади сечения S, градиенту температуры
, пропорционально площади сечения S, градиенту температуры 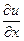 и промежутку времени
и промежутку времени 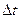 :
: 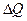 ~
~ 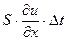 .
.
Если с S и 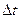 все очевидно, то появление
все очевидно, то появление 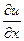 требует пояснений. Из экспериментов известно, что поток тепла
требует пояснений. Из экспериментов известно, что поток тепла 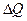 через некоторый участок стержня длиной
через некоторый участок стержня длиной 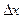 тем больше, чем больше разность температур
тем больше, чем больше разность температур 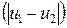 на его концах и чем меньше расстояние
на его концах и чем меньше расстояние 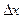 :
:
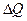 ~
~ 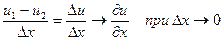

Вводя коэффициент пропорциональности k, называемый коэффициентом теплопроводности, получаем
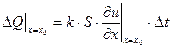 (1)
(1)
Значение k определяется материалом стержня в единицах системы СИ:
| материал | Теплопроводность (Вт/м·К) |
| Медь Сталь Кирпич Дерево Воздух | 0,7 0,1 0,034 |
Таким образом, различия в теплопроводности разных материалов огромны.
Теперь запишем количество тепла, проходящее через сечение в точке 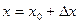 . Оно определяется той же формулой:
. Оно определяется той же формулой:
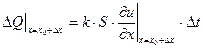
с условием, что производная 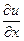 берется в точке
берется в точке 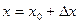 . Для получения искомого уравнения ее надо выразить через значение в точке х0.
. Для получения искомого уравнения ее надо выразить через значение в точке х0.
Имеем разложение в ряд, ограничиваясь первым порядком приращения 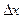 ,
,
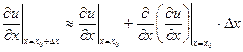
в силу чего получим:
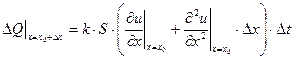 (2)
(2)
Из (1) и (2) видно, что через сечения 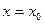 и
и 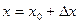 за время
за время 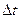 прошло разное количество тепла, поэтому та его часть, которая пошла на нагревание (или, в зависимости от знака, на охлаждение) этого участка стержня, есть
прошло разное количество тепла, поэтому та его часть, которая пошла на нагревание (или, в зависимости от знака, на охлаждение) этого участка стержня, есть
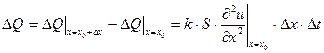
Пусть за то же время температура участка изменилась на 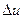 ; как известно, это связано с изменением тепла
; как известно, это связано с изменением тепла 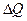 , которое выражается соотношением:
, которое выражается соотношением:
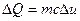 ,
,
где m – масса, c – удельная теплоемкость. Приравняем два выражения для 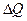 :
:
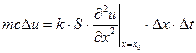
Поскольку массу можно представить как 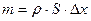 (ρ – плотность вещества), то, поделив обе части уравнения на
(ρ – плотность вещества), то, поделив обе части уравнения на 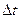 и перейдя к пределу при
и перейдя к пределу при 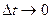 , получим
, получим
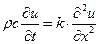 .
.
В это выражение входят три постоянные, характеризующие вещество. Удобно объединить их в одну постоянную 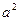 , где
, где 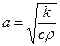 -- так называемый, коэффициент температуропроводности. Обозначение
-- так называемый, коэффициент температуропроводности. Обозначение 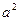 удобно, так как фиксирует знак этого коэффициента – он всегда положителен.
удобно, так как фиксирует знак этого коэффициента – он всегда положителен.
Тогда перепишем уравнение в виде
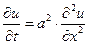 (3)
(3)
Это – основное уравнение теплопроводности для однородного стержня. Как следует из процедуры вывода, это уравнение локально, т.е. в данный момент времени и в данной точке выражает закон сохранения энергии.
Уравнение (3) – одно из самых простых дифференциальных уравнений в частных производных. Несмотря на его элементарный вид, решение такого уравнения даже в простейшей ситуации есть весьма сложная задача.
Начальные и краевые условия. Уравнение (3) описывает процесс изменения температуры стержня во времени и в пространстве. Для решения задачи надо знать распределение температуры в теле в некоторый начальный момент времени:
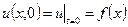 ,(4)
,(4)
где 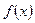 --заданная функция.Кроме того, в тех местах, где возможен теплообмен с окружающей средой, надо знать условия этого теплообмена. Для стержня с теплоизолированной боковой поверхностью такими местами являются концы. Пусть длина стержня l. Если один конец имеет координату х = 0, а другой – х = l, то простейший вариант краевых условий – постоянная температура на каждом конце стержня:
--заданная функция.Кроме того, в тех местах, где возможен теплообмен с окружающей средой, надо знать условия этого теплообмена. Для стержня с теплоизолированной боковой поверхностью такими местами являются концы. Пусть длина стержня l. Если один конец имеет координату х = 0, а другой – х = l, то простейший вариант краевых условий – постоянная температура на каждом конце стержня:
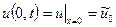 ,
, 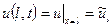 (5)
(5)
Нижеследующее утверждение физически очевидно, но его строгое математическое доказательство весьма непросто: дифференциальное уравнение (3) при начальном условии (4) и краевых условиях (5) имеет единственное решение.
Аналитические методы решения задачи одномерной теплопроводности существуют, но требуют значительной математической подготовки. Решение обычно получается в виде ряда Фурье, однако по его виду протекание процесса неочевидно, оно требует визуализации на компьютере. В двух- и трехмерном случаях аналитическое решение чаще всего получить не удается. Решим задачу численно, используя вычислительный эксперимент.
Используем методы конечных разностей. Покажем на примере уравнения теплопроводности наиболее распространенные методы численного интегрирования уравнений в частных производных. В их основе лежит прием дискретизации.
Покроем отрезок стержня [0, l] одномерной сеткой (т.е. разобьем на n равных частей) с узлами в точках
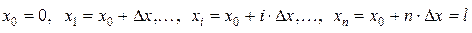
Искомую функцию u(x) будем аппроксимировать ее значениями в узлах сетки.
Остановимся на разностной аппроксимации производных. Производная 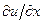 связывает значения
связывает значения 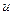 в соседних узлах сетки. Очевидная аппроксимация первой производной в точке
в соседних узлах сетки. Очевидная аппроксимация первой производной в точке 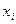 имеет вид
имеет вид
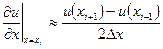 (6)
(6)
Для крайних точек, однако, такая аппроксимация невозможна, и простейший способ – ограничиться односторонними разностями:
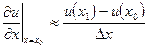 ,
, 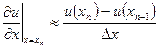 (7)
(7)
Выражения (6) и (7) дают простейшие аппроксимации. Рассматривая большее количество узлов, можно получить аппроксимации более высокого порядка. Аппроксимация вторых производных имеет вид
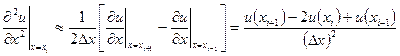 , i = 1, 2, …, n – 1 (8)
, i = 1, 2, …, n – 1 (8)
В уравнении (3) есть производная по t: 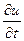 . Для нее также нужна аппроксимация, поэтому возникает еще одна – временная сетка. При интегрировании уравнений по времени мы движемся по отдельным временным слоям, а в каждом слое определяем значения искомой функции на пространственной сетке. Если для интегрирования по времени используется метод Эйлера или другой одношаговый метод, то для работы со следующим временным слоем используются значения искомой функции из предыдущего слоя (для более сложных методов – из нескольких предыдущих слоев).
. Для нее также нужна аппроксимация, поэтому возникает еще одна – временная сетка. При интегрировании уравнений по времени мы движемся по отдельным временным слоям, а в каждом слое определяем значения искомой функции на пространственной сетке. Если для интегрирования по времени используется метод Эйлера или другой одношаговый метод, то для работы со следующим временным слоем используются значения искомой функции из предыдущего слоя (для более сложных методов – из нескольких предыдущих слоев).
Далее будем индексы, соответствующие временной сетке, писать вверху (надстрочно), а пространственной – внизу (подстрочно). Таким образом, для одномерного уравнения запись 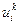 означает значение функции
означает значение функции 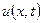 в k-м временном слое и в i-м узле пространственной сетки.
в k-м временном слое и в i-м узле пространственной сетки.
Рассмотрим уравнение теплопроводности (3) и сформулируем простейшую возможную схему его интегрирования – явную схему первого порядка – по времени, используя метод Эйлера. По пространству – используем простейшие аппроксимации (8). Шаг по времени обозначим 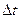 , по координате –
, по координате – 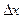 .
.
Температуру на новом временном слое для внутренних узлов выразим через температуру на предыдущем временном слое, т.е. 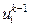 через
через 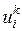 .
.
Запишем уравнение (3) для дискретной функции 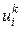 :
:
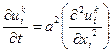
Обозначим правую часть уравнения (3) для дискретной функции 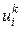 :
:
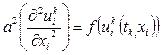
Запишем метод Эйлера для функции 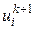 на новом временном слое k+1 с использованием аппроксимации (8):
на новом временном слое k+1 с использованием аппроксимации (8):
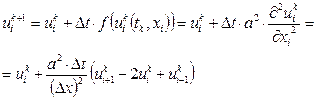
В итоге получим
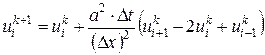 (9)
(9)
Это явная разностная схема по времени. Она записана для внутренних узлов сетки. Здесь k = 0, 1, …; i = 1, 2, …, n – 1 (краевые точки i=0, i=n не включены).
В силу начального условия (4) в начальный момент времени (при k=0):
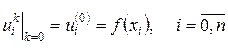
где функция 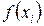 задана и определяет значение температуры на нулевом слое.
задана и определяет значение температуры на нулевом слое.
Значения на концах стержня 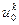 и
и 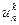 зависят от типа краевого условия (5), когда концы стержня поддерживаются при постоянной температуре, имеем:
зависят от типа краевого условия (5), когда концы стержня поддерживаются при постоянной температуре, имеем:
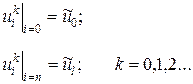
где 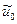 ,
, 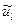 -- заданные числа.
-- заданные числа.
Теперь остановимся на вопросе об устойчивости и эффективности метода. Поскольку схема (9) явная, тo она относится к условно устойчивым разностным схемам. Существуют разностные схемы:
§ абсолютно неустойчивые,
§ абсолютно устойчивые
§ условно устойчивые.
Первые при любых, сколь угодно малых, шагах так «раскачивают» начальную погрешность, что приводят к результатам, не имеющим общего с реальностью.
Вторые ни при каких шагах не «раскачиваются», хотя, конечно, чем меньше шаг, тем меньше разница между приближенными и точными решениями.
Третьи устойчивы при одних комбинациях значений 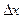 и
и 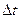 и неустойчивы при других. Доказано, что разностная схема (9) устойчива при
и неустойчивы при других. Доказано, что разностная схема (9) устойчива при
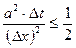 (10)
(10)
и неустойчива в противном случае.
Дата добавления: 2015-01-13; просмотров: 3480;
