АНАЛИЗ ДИСКРЕТНОЙ СПР С ПЕРХОДНЫМИ ПРОЦЕССАМИ КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ
Определение передаточной функции дискретной СПР

Рисунок 8 – Схема дискретной СПР с переходными процессами конечной длительности
Определим ПФ дискретной системы:
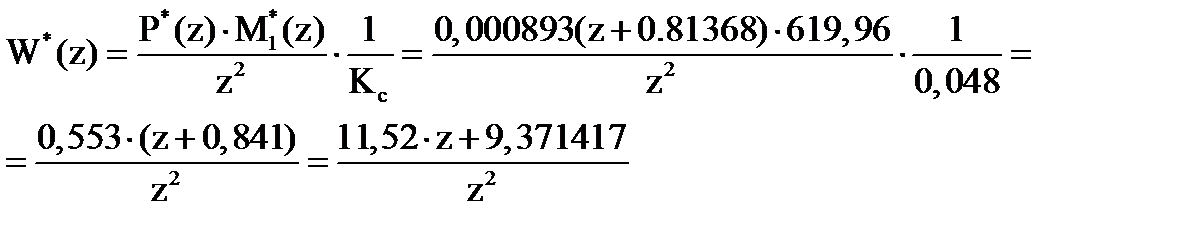
Определение устойчивости дискретной СПР по корням характеристического уравнения в плоскостях «z» и «w»
Характеристический полином дискретной СПР имеет вид:

Определим корни характеристического уравнения дискретной СПР в программной среде Mathcad:

Построим корни характеристического полинома в плоскости «z»
(рисунок 9).

Рисунок 9 – Корни характеристического полинома дискретной СПР в
плоскости «z»
Определим ПФ дискретной СПР от переменной w:
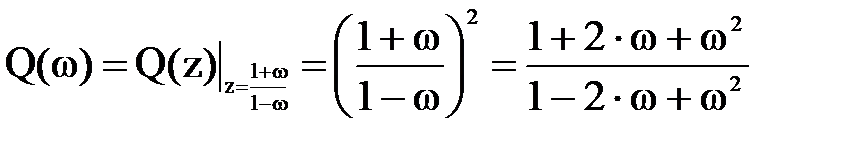
Определим корни характеристического уравнения дискретной СПР в плоскости «w» в программной среде Mathcad:



Корни действительные отрицательные, лежат в левой полуплоскости. Значит система устойчивая.
Построим корни характеристического полинома в плоскости «w»
(рисунок 10).

Рисунок 10 – Корни характеристического полинома замкнутой дискретной СПР в плоскости «w»
Нахождение уравнения переходного процесса и показателей качества при реакции дискретной СПР на единичное ступенчатое воздействие
Построение переходного процесса в цифровой СПР по разностному уравнению
Определим реакцию системы на единичное ступенчатое воздействие:
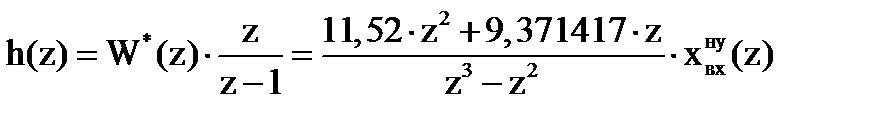
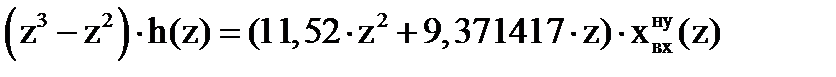
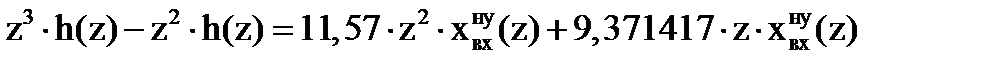
Так как оператор z даёт отсчёт на один такт вперед, принимаем
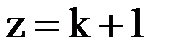
Перепишем равенство:
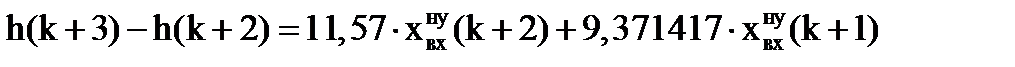
Принимаем
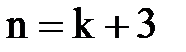 ,
,
тогда полученное равенство примет вид:
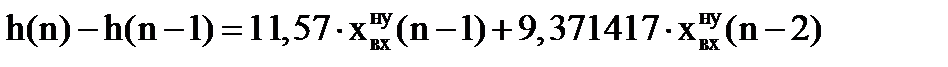
Отсюда определим функцию выходной координаты:
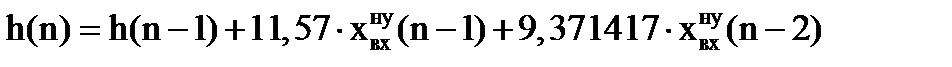
|
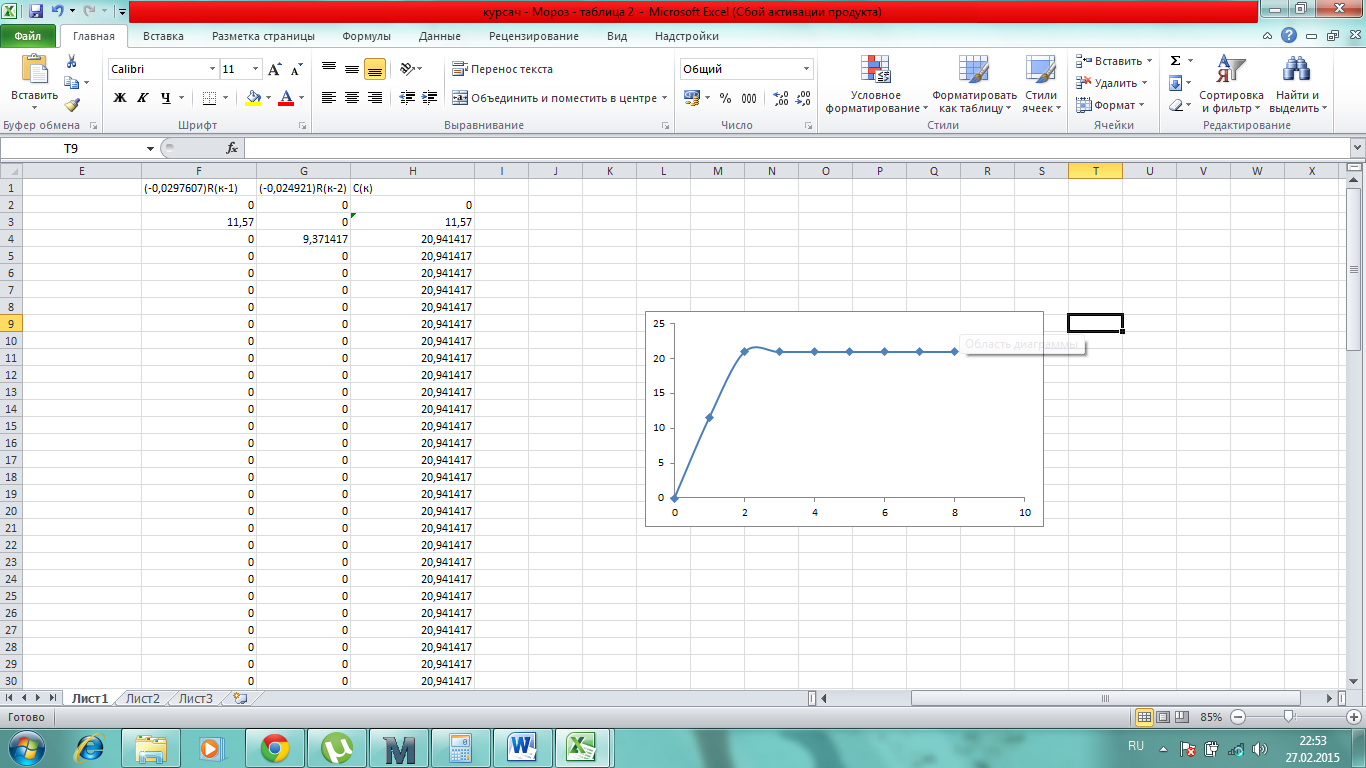
График переходного процесса
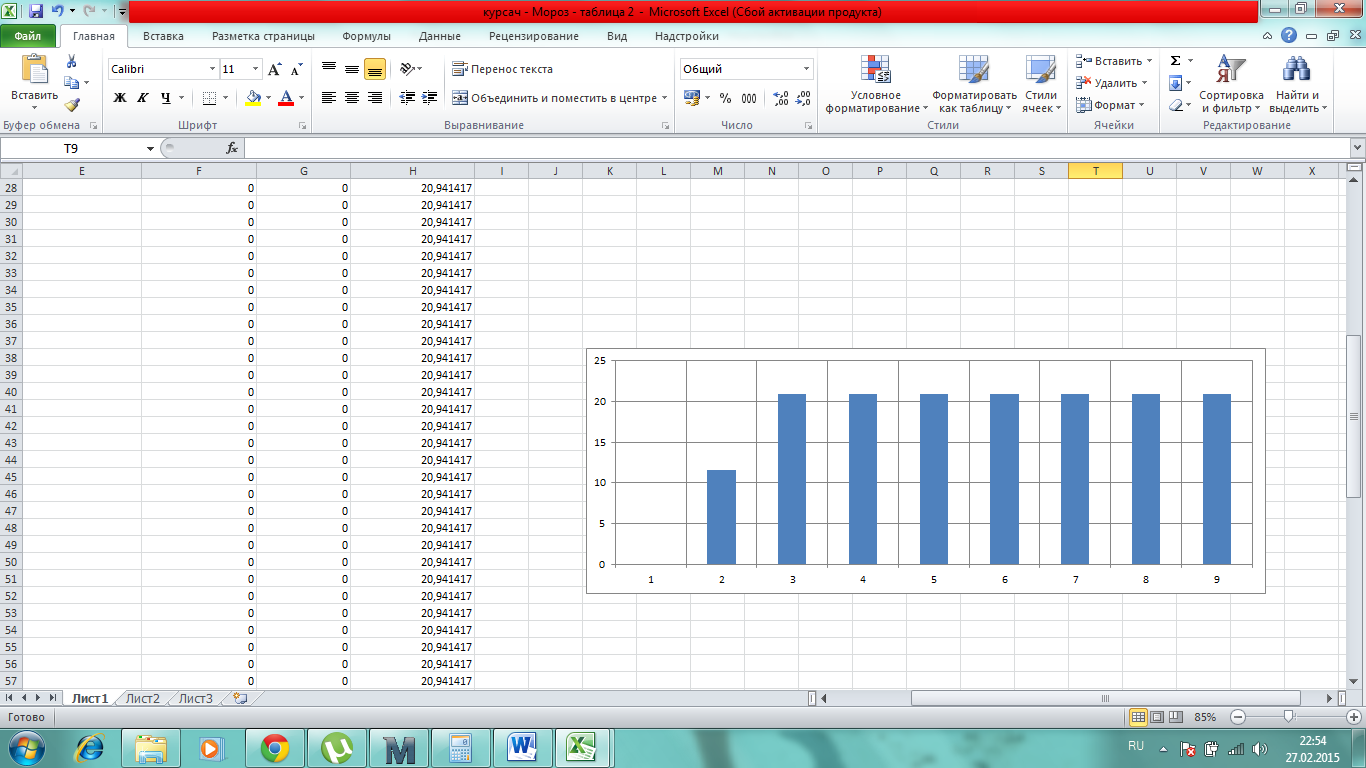
График переходного процесса
Построение переходного процесса в цифровой СПР в среде MatLab Simulink
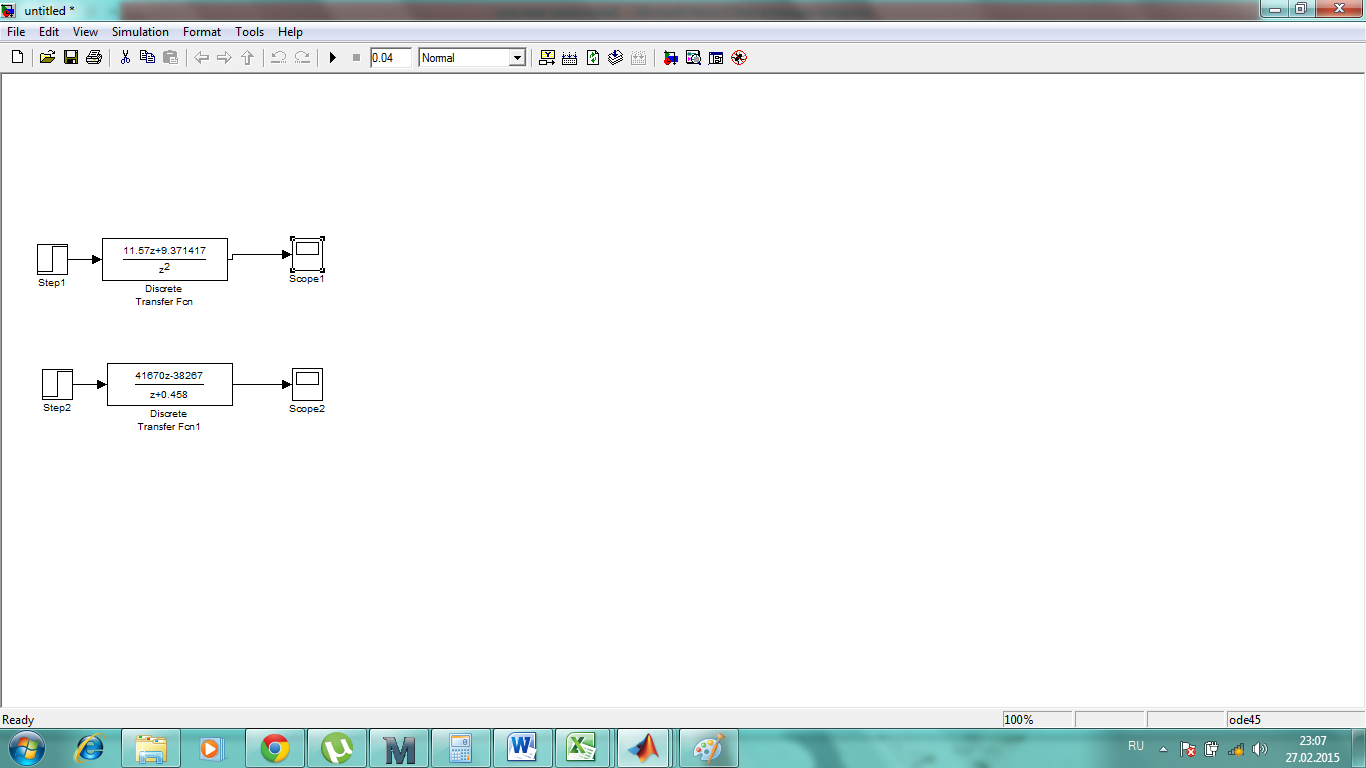
Рисунок 12 – Модель дискретной СПР в программе Matlab Simulink
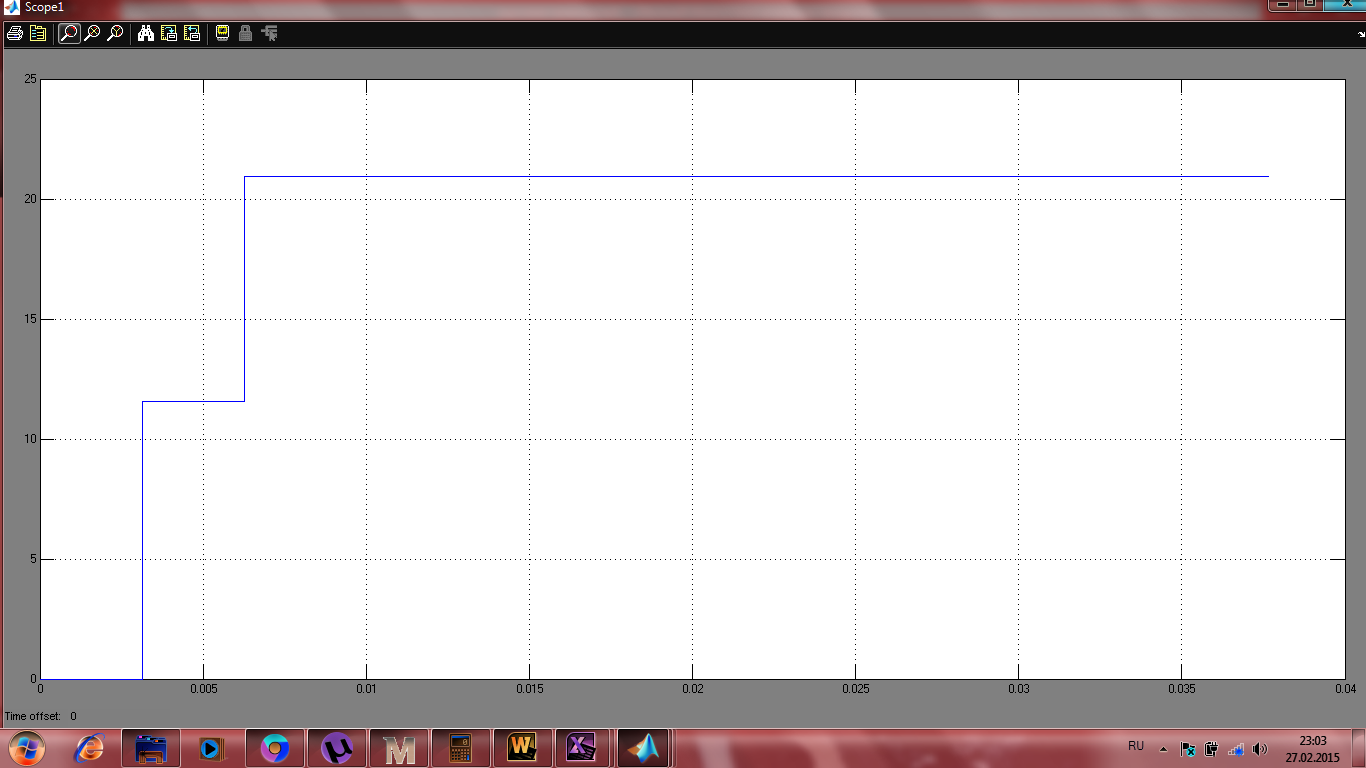
Рисунок 13 – График переходного момента скорости АД дискретной СПР
Определение показателей качества
Определим показатели качества дискретной СПР:
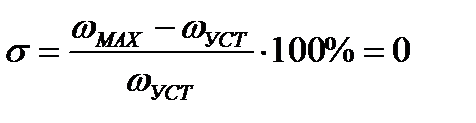
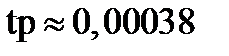

Дата добавления: 2015-02-28; просмотров: 1469;
