АНАЛИЗ НЕПРЕРЫВНОЙ МОДЕЛИ СПР, НАСТРОЕННОЙ НА МОДУЛЬНЫЙ ОПТИМУМ
Определение передаточной функции СПР
Определим ПФ замкнутого скорректированного контура скорости:
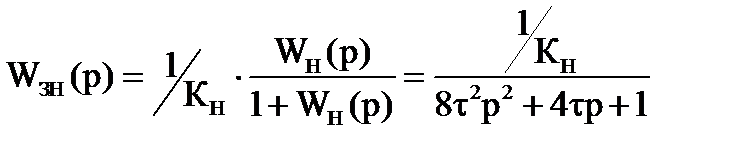
Определим ПФ замкнутой скорректированной системы:

Проверка устойчивости СПР по корням характеристического уравнения в плоскости «p»
Определим корни характеристического уравнения замкнутой скорректированной системы в программной среде Mathcad:
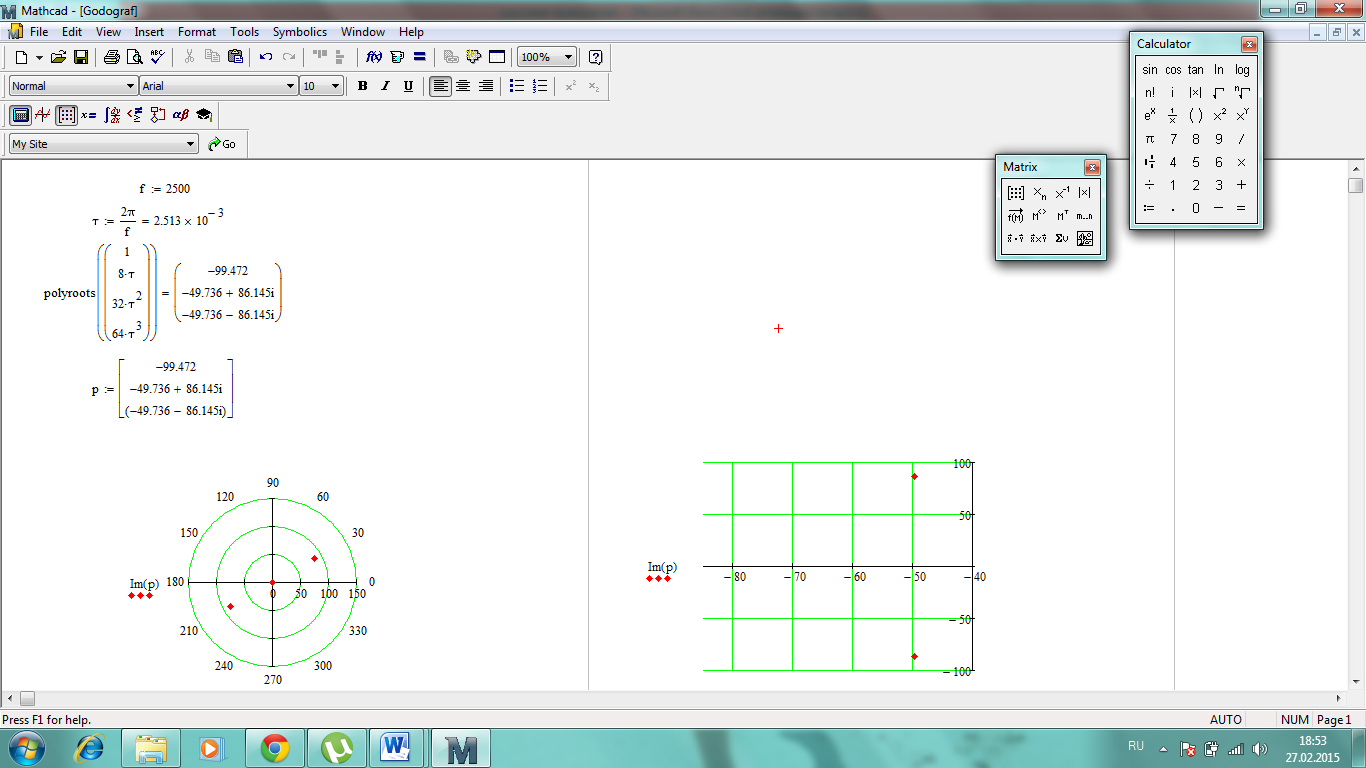
Корни – левые, действительная часть отрицательная. Значит система устойчивая.
Определим степень коллебательности:
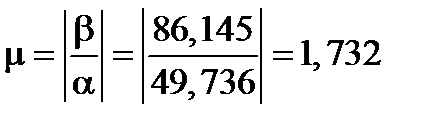
Построим корни характеристического полинома в плоскости «р» (рисунок 2).
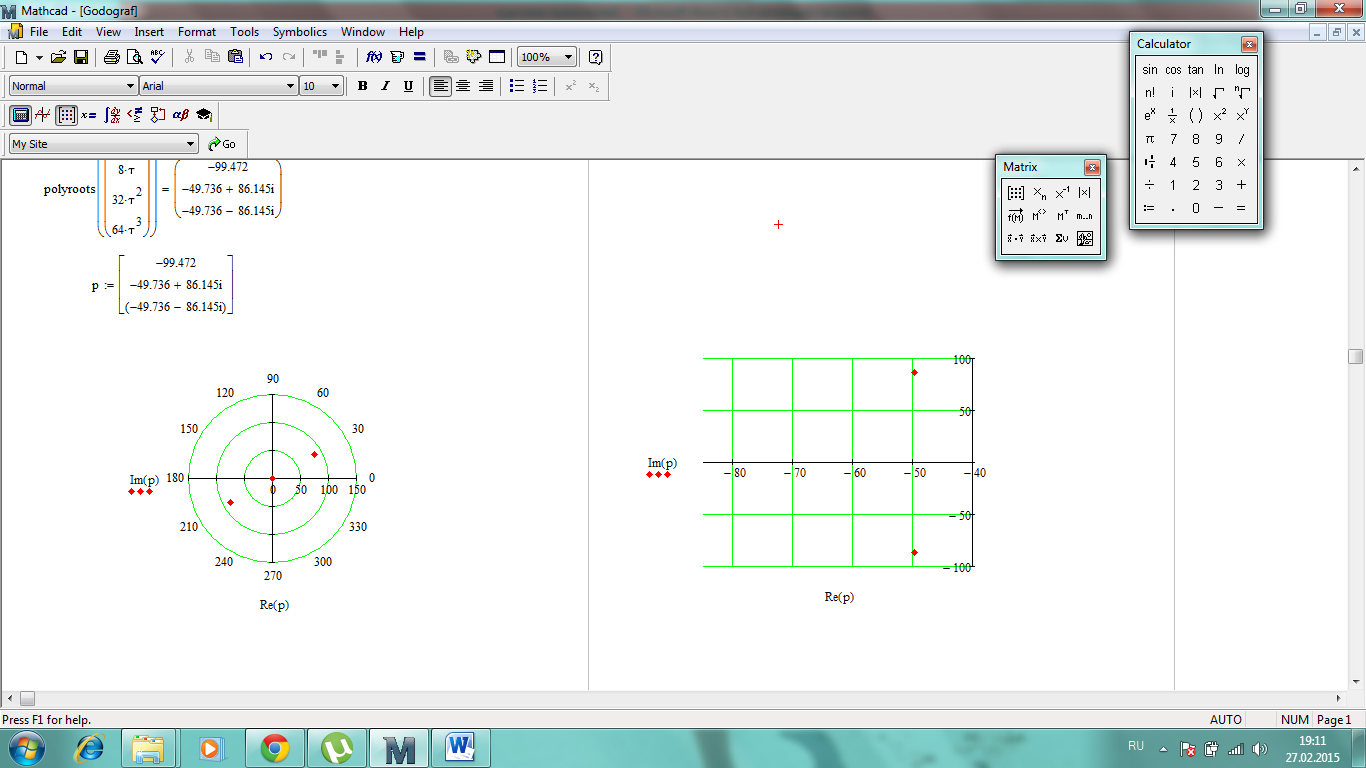
Рисунок 2 – Корни характеристического полинома замкнутой скорректированной системы в плоскости «р»
Нахождение уравнения переходного процесса и показателей качества при реакции СПР на единичное ступенчатое воздействие
Запишем функцию переходного процесса при реакции на единичное ступенчатое воздействие:


Произведем обратное преобразование Лапласа в программной среде Mathcad:
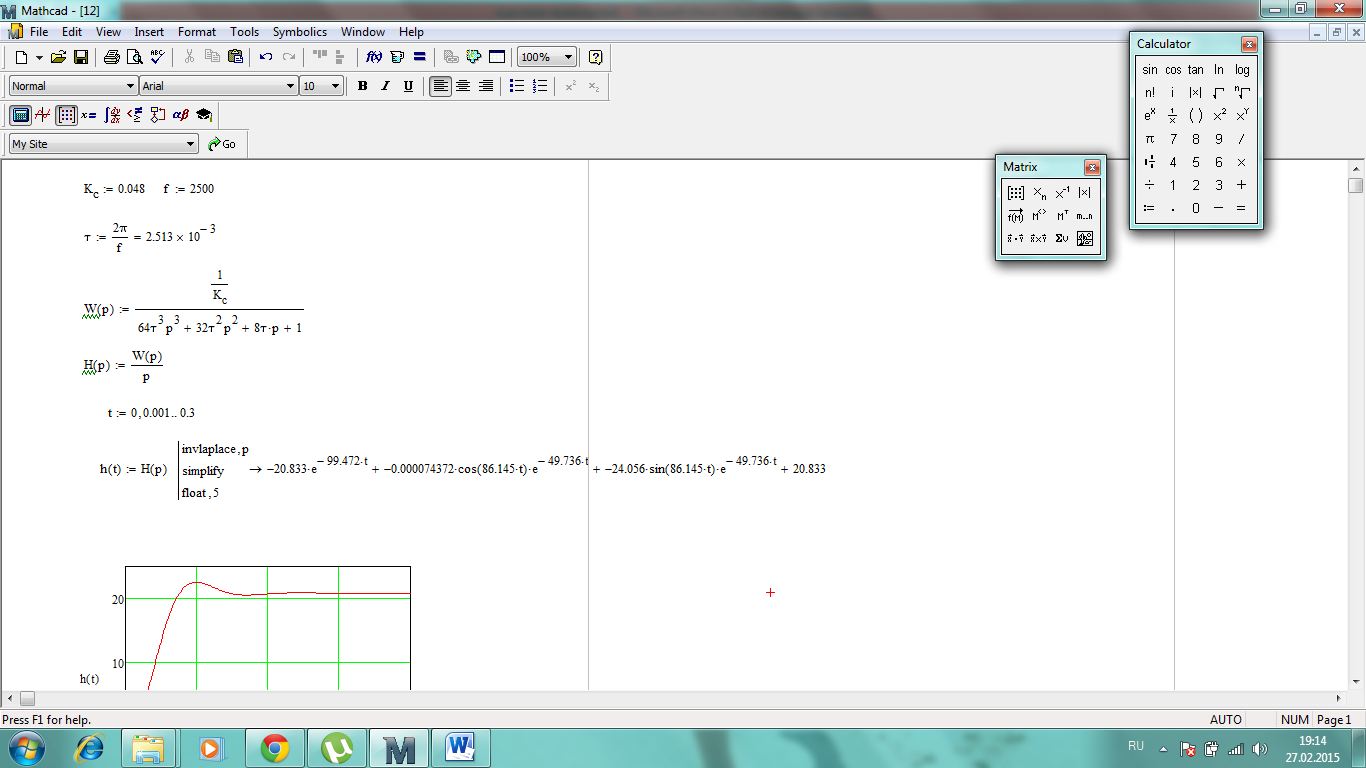
Построим переходный процесс замкнутой скорректированной системы при реакции на единичное ступенчатое воздействие (рисунок 3).
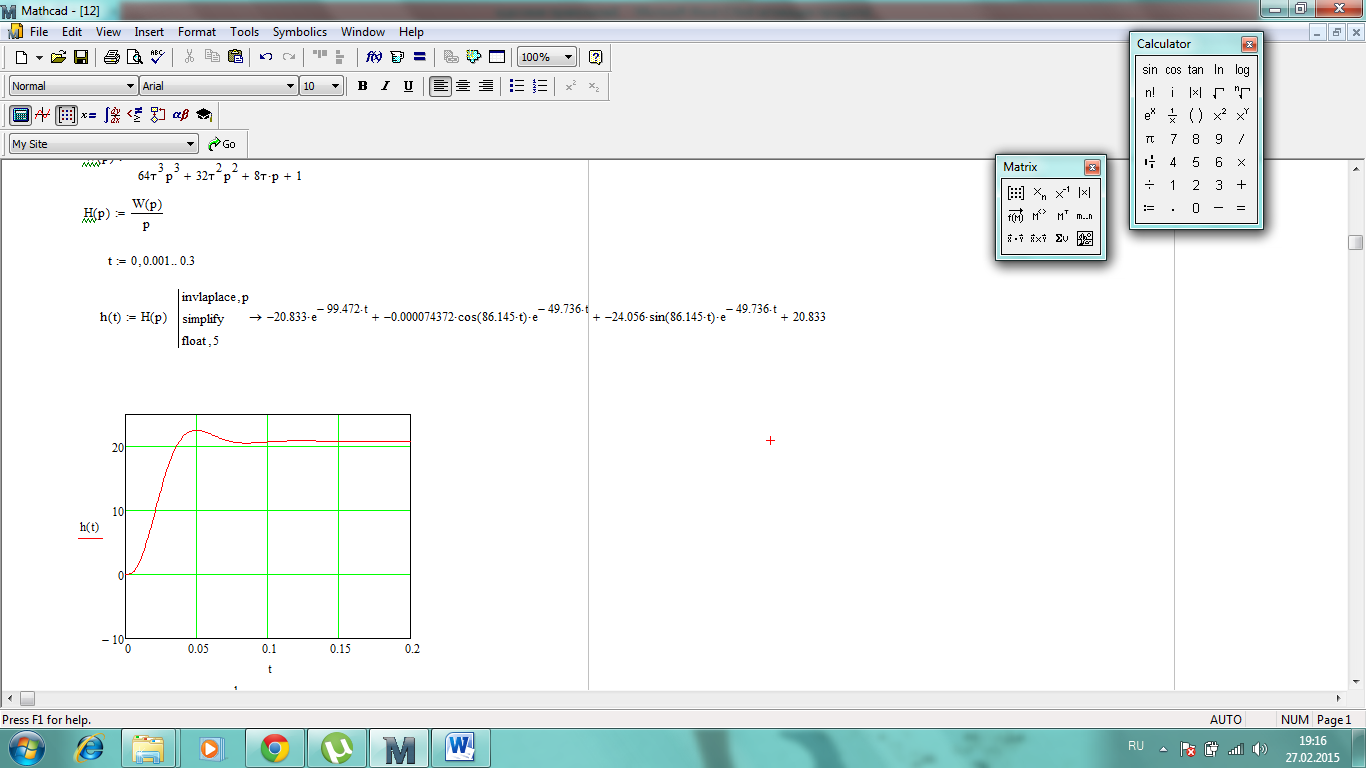
Рисунок 3 – График переходного процесса замкнутой скорректированной системы при реакции на единичное ступенчатое воздействие
Определим показатели качества. Рассчитаем перерегулирование:
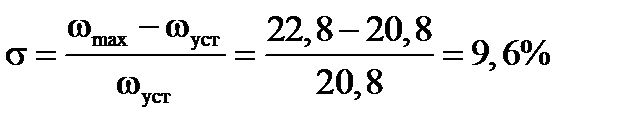
Время регулирования (вхождение в пятипроцентную зону): 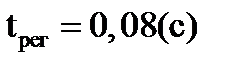
Дата добавления: 2015-02-28; просмотров: 1434;
