ДВИЖЕНИЕ ТЕЛА С ПЕРЕМЕННОЙ МАССОЙ: ВЗЛЕТ РАКЕТЫ

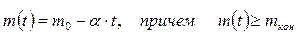Построим простейшую модель вертикального взлета ракеты. Примем гипотезу, что ее масса уменьшается во время взлета по линейному закону (масса меняется со временем):

где 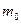-- начальная масса ракеты, 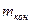-- конечная масса (т.е. масса полезного груза, выводимого на орбиту), α – расход топлива.

Это допущение согласуется с допущением о постоянной силе тяги.

В данной задаче нельзя пренебречь убыванием массы ракеты в процессе взлета – оно огромно и составляет большую часть исходной массы.

У одной из крупнейших отечественных ракет «Энергия» стартовая масса составляет 20000 тонн, а к концу взлета всего 200 тонн.

Поиск математического описания проблемы не составляет труда – в его основе все тот же второй закон Ньютона. Поскольку ракета очень быстро набирает высокую скорость, то линейной составляющей 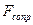можно пренебречь. Тогда 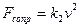, и уравнение для скорости в проекции на вертикальную ось принимает вид

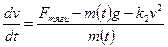(1)

В коэффициент 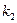входит величина 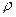– плотность окружающей среды, которая на «космических» высотах во много раз меньше, чем на поверхности земли. На высоте 5.5 км плотность воздуха вдвое меньше, чем у поверхности, на высоте 11 км – в четыре раза меньше. Поэтому математически зависимость плотности атмосферы от высоты записывается формулой

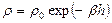
где 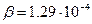, 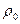- плотность воздуха вблизи поверхности Земли, высота h измеряется в метрах. Поскольку величина h меняется в ходе полета, уравнение для изменения h(t) следует добавить к уравнению (1) и записать следующую систему дифференциальных уравнений:

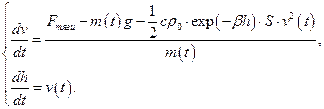(2)

где с – коэффициент лобового сопротивления, S – площадь поперечного сечения.