Вариации массовых явлений. Построение вариационного ряда
Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Как мы уже говорили ранее, в зависимости от того, является признак, взятый за основу группировки, качественным или количественным, различают соответственно два типа рядов распределения – атрибутивные и вариационные. Ряды распределения, построенные по качественному признаку, называют атрибутивными. Примером атрибутивных рядов может служить распределение населения по полу, характеру труда, национальности, профессии и т.д. Ряды распределения, построенные по количественному признаку, называют вариационными.
Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц совокупности в один и тот же период или момент времени.
Не следует путать вариацию признака в совокупности и изменения этого признака у одной и той же единицы в разные периоды времени. В отличие от вариации различия признака у одного и того же объекта, у одной и той же единицы совокупности в разные периоды или моменты времени следует называть изменениями во времени и колебаниями. Методы их измерения и изучения принципиально отличаются от методов измерения вариации.
Причиной вариации являются разные условия существования разных единиц совокупности. При изучении вариации можно выделить две группы факторов, которые формируют различный уровень признака в исследуемой совокупности. Первую группу составляют факторы, общие для всех единиц совокупности. Во вторую группу входят факторы, свойственные конкретным единицам совокупности и определяющие индивидуальные особенности.
Вариация присуща всем без исключения явлениям природы и общества, кроме законодательно закрепленных нормативных значений отдельных социальных признаков: не варьирует признак "число председателей правительства" - он всегда один. Не варьирующие признаки не представляют интереса для статистики; предметом изучения статистики является вариация. Большинство методов статистики - это либо методы измерения вариации, либо методы абстрагирования от неё.
Вариация, несомненно, необходимое условие существования и развития массовых явлений. Например, вариация геномов (наборов генов) родительских организмов растений и животных обеспечивает жизнеспособность потомства. В тоже время известно, что нельзя получить потомство от организмов со слишком разными свойствами - разных видов, родов и семейств. Чрезмерная вариация генотипов препятствует развитию. И в промышленном производстве, особенно массовом, вариации размеров, свойств деталей, из которых собирается автомашина, телевизор и т.д. должна быть введена в жесткие рамки "допусков", чтобы сборка была возможной и не страдало качество.
Итак, в жизни общества, как и в природе, каждой массовой совокупности, массовому процессу присуща некоторая специфическая мера вариации её элементов, при которой данный процесс протекает оптимально.
Чтобы руководитель предприятия, менеджер могли управлять вариацией и изучать её, статистикой разработаны специальные методы исследования вариации. Система показателей, с помощью которой вариация измеряется, характеризуется её свойства.
Первым этапом статистического изучения вариации является построение вариационного ряда - упорядоченного распределения единиц совокупности по возрастающим или по убывающим значениям признака и подсчет числа единиц с тем или иным значением признака.
Существуют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд. Вариационный ряд часто называют рядом распределения. Этот термин используется при изучении вариации как количественных, так и неколичественных признаков. Ряд представляет собой структурную группировку.
Ранжированный ряд - это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
Например, следующая таблица "Крупные банки Санкт-Петербурга, ранжированные по размерам собственного капитала на 01.07.96 г."
| Название банка | Собственный капитал, млрд. руб. |
| Петроагропромбанк | |
| Петровский | |
| Балтийский | |
| Банк Санкт-Петербург | |
| Промстройбанк |
Если численность единиц совокупности достаточно велика, ранжированный ряд становится громоздким, а его построение требует длительное время. В таких случаях вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.
Если признак принимает небольшое число значений, строится дискретный вариационный ряд. Примером такого ряда может служить таблица распределения футбольных матчей по числу забитых мячей. Дискретный вариационный ряд - это таблица, состоящая из двух строк или граф: конкретных значений варьирующего признака xi и числа единиц совокупности с данным значением признака fi - частот.
Число групп в дискретном вариационном ряду определяется числом реально существующих значений варьирующего признака. Если же признак может принимать хотя и дискретные значения, но их число очень велико (например, поголовье скота на 1 января года в разных с/х предприятиях может составлять от нуля до десятков тысяч голов), тогда строиться интервальный вариационный ряд. Интервальный вариационный ряд строиться и для изучения признаков, которые могут принимать любые, как целые, так и дробные, значения в области своего существования. Таковы, например, рентабельность реализованной продукции, себестоимость единицы продукции, доход на 1 жителя города, доля лиц с высшим образованием среди населения разных территорий и вообще все вторичные признаки, значения которых рассчитываются путем деления величины одного первичного признака на величину другого.
Интервальный вариационный ряд представляет собой таблицу, состоящую из двух граф (или строк) - интервалов признака, вариация которого изучается, и числа единиц совокупности, попадающих в данный интервал, или долей этого числа от общей численности совокупности.
При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервальный признак) и установить величину интервала. Поскольку при анализе вариационного ряда сравнивают частоты в разных интервалах, необходимо, чтобы величина интервала была постоянной. Оптимальное число групп выбирается так, чтобы в достаточной мере отразилось разнообразие значений признака в совокупности и в то же время закономерность распределения, его форма не искажались случайными колебаниями частот. Если групп будет слишком мало не проявиться закономерность вариации.
Число групп в вариационном ряду устанавливают по формуле Стерджесса:
k ≈ 1 + 3,332 ∙ lg n = 1+ 1,441 ln n,
где к число групп, n - численность совокупности.
Определение величины интервала. Зная число групп, рассчитывают величину равных интервалов:
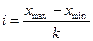
Рассмотрим пример построения интервального вариационного ряда. Допустим, нам необходимо построить вариационный ряд распределения предприятий области по урожайности зерновых культур за какой-то год. Число с/х предприятий, имевших посевы зерновых культур, составило 143; наименьшее значение урожайности равно 10,7 ц/га, наибольшее - 53,1 ц/га. Имеем: k = 1+3,322 ∙ lg 143 = 8,16. Так как число групп целое, следовательно, рекомендуется построить 8 или 9 групп.
При 8 группах величина интервала составляет: i = (53,1 - 10,7) : 8 = 5,3 ц/га; при 9 группах i = (53,1 - 10,7) : 9 = 4,7 ц/га.
Границы интервалов могут указываться разным образом: верхняя граница предыдущего интервала повторяет нижнюю границу следующего, или не повторяет (Например, интервалы: 10-15, 15-20, 20-25 и т.д. или 10 -15, 15,1 -20, 20,1 - 25 и т.д.) Но во втором случае тогда возникает осложнения с серединой интервала. Поэтому предпочтительнее ставить интервалы с повторяющейся округленной границей и единицу совокупности, имеющей значение равное границе интервала включать в тот интервал, где это точное значение впервые указывается.
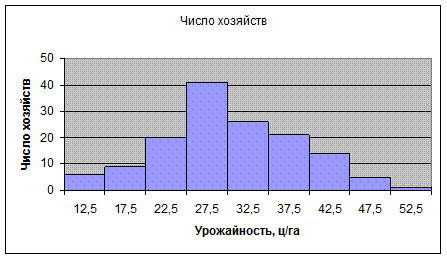
Существенную помощь в анализе вариационного ряда и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные по оси абсцисс, - это интервалы значений варьирующего признака, а высоты столбиков - частоты, соответствующие масштабу по оси ординат. Диаграммы этого рода часто называют гистограммами.
|
На данном рисунке представлен вариационный ряд распределения с/х предприятий по урожайности зерновых культур. Данное распределение показывает характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов признака, реже – крайние, малые и большие значения признака. если имеется дискретный вариационный ряд или используются середины интервалов, то графическое изображение такого ряда называется полигоном.
Рассмотрим наш пример с хозяйствами и построим вариационный ряд с рассчитанными интервалами (количество групп - 9, округлим интервал до 5 ц/га). Получаем следующую таблицу:
| Группы хозяйств по урожайности, ц/га xi | Число хозяйств fi | Середина интервала, ц/га xi' | xi' fi | Накопленная частота fi' |
| 10-15 | 12,5 | 75,0 | ||
| 15-20 | 17,5 | 157,5 | ||
| 20-25 | 22,5 | 450,0 | ||
| 25-30 | 27.5 | 1127,5 | ||
| 30-35 | 32,5 | 845,0 | ||
| 35-40 | 37.5 | 787,5 | ||
| 40-45 | 42,5 | 595,0 | ||
| 45-50 | 47,5 | 237,5 | ||
| 50-55 | 52,5 | 52,5 | ||
| Итого | 4327,5 |
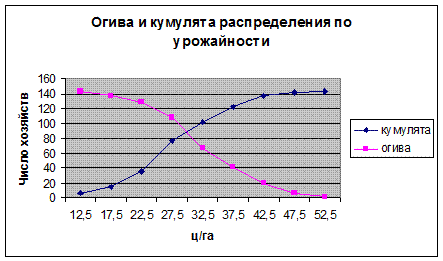
Графа 5 этой таблицы называется рядом накопленных частот. Этот ряд значений числа единиц совокупности с меньшими и равными нижней границе соответствующего интервала значениями признака. Такой ряд называют еще кумулятивным. Можно построить кумулятивное распределение "не меньше, чем", а можно "больше чем". В первом случае график кумулятивного распределения называют кумулятой, во втором - огивой.
Графики будут выглядеть следующим образом:
|
Если в таблице число хозяйств с тем или иным уровнем урожайности выразить в процентах к итогу, принимая все число хозяйств (143) за 100%, то средняя урожайность может быть вычислена так:
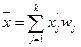
где wi - частость i-той категории вариационного ряда
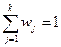 (или 100%)
(или 100%)
Если приходится иметь дело с вариационным рядом с неравными интервалами, то для сопоставимости нужно частоты привести к единице интервала. Полученное отношение называется плотностью распределения:
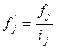 или
или 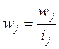
где fj' - абсолютная плотность распределения в j-м интервале;
w'j - относительная плотность распределения в j-м интервале
ij - ширина j-го интервала.
Плотность распределения используется как для расчета обобщающих показателей, так и для графического изображения вариационных рядов с неравными интервалами.
Дата добавления: 2015-03-03; просмотров: 2947;