Средняя геометрическая величина

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то применяют среднюю геометрическую величину. Её формула такова:

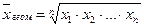
Основное применение геометрическая средняя находит при определении средних темпов роста. Пусть, например, в результате инфляции за первый год цена товара возросла в 2 раза к предыдущему году, а за второй год еще в три раза к уровню предыдущего года. Ясно, что за 2 года цена выросла в 6 раз. Каков средний темп роста цены за год? Арифметическая средняя здесь непригодна, так как если за год цены бы возросли в (2+3) : 2 = 2,5 раза, то за два года цена бы возросла бы в 2,5 *2,5 = 6,25 раза, а не в 6 раз. Геометрическая средняя дает правильный ответ: √6 = 2,45 раза (2,45 * 2,45 = 6,0025).

Геометрическая средняя величина дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака.