В уравнении жесткого приведенного механического звена величина
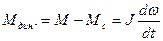
определяет собой суммарную динамическую нагрузку. Знак Мдин. Зависит от знака ускорения. При 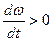 Мдин. совпадает со знаком скорости w, а при
Мдин. совпадает со знаком скорости w, а при 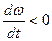 - противоположен знаку скорости. При ускорении системы Мдин. является тормозным по отношению к моменту М двигателя, а при замедлении – является движущим и совпадает с направлением момента двигателя. Освобождающаяся при снижении скорости кинетическая энергия расходуется на совершение работы по преодолению результирующего М-Мс, который в этом случае является тормозным.
- противоположен знаку скорости. При ускорении системы Мдин. является тормозным по отношению к моменту М двигателя, а при замедлении – является движущим и совпадает с направлением момента двигателя. Освобождающаяся при снижении скорости кинетическая энергия расходуется на совершение работы по преодолению результирующего М-Мс, который в этом случае является тормозным.
Максимальная полная нагрузка двигателя, определяемая суммой максимальной статической и динамической нагрузок, определяет кратковременную перегрузку двигателя и не должна превышать допустимой перегрузочной способности двигателя:
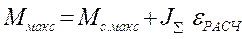 , где
, где
eрасч – расчетное заданное ускорение.
Динамический момент Мдин при пуске частично затрачивается на ускорение ротора (якоря) двигателя, а в остальной части через передачи воздействует на механизм, ускоряя его массы и совершая работу по увеличению в них запаса кинетической энергии. Следовательно, динамическая нагрузка при пуске увеличивает полную нагрузку передач на величину динамического момента механизма. В жесткой двухмассовой механической системе при J2>>J1 это увеличение может быть значительным, а при J2<J1 основной нагрузкой передач является статическая нагрузка. Во всех случаях динамические нагрузки передач и элементов кинематической цепи механизма могут существенно дополнительно увеличиваться при возникновении в системе упругих механических колебаний.
Правильное определение динамических нагрузок передач эл.привода имеет важное практическое значение. Нагрузки определяют износ механического оборудования, причем наиболее неблагоприятно влияние нагрузок, содержащих знакопеременную составляющую. Поэтому ограничение максимальных и уменьшение колебательных нагрузок повышает надежность и долговечность механической части электропривода и механизма.
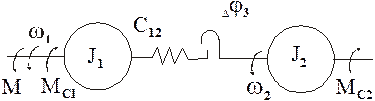 |
Динамические нагрузки механического оборудования значительно возрастают из-за ударов, возникающих при выборе зазоров в передачах и сочленения машин. С учетом кинематических зазоров расчетная схема 2-х массовой упругой механической системы может быть представлена в следующем виде:
При наличии зазора Dj3 зависимость момента М12 упругого взаимодействия 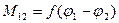 становится нелинейной и принимает вид, изображенный на следующем рис.
становится нелинейной и принимает вид, изображенный на следующем рис.
Уравнения движения в этом случае запишутся в виде:
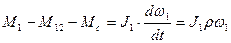
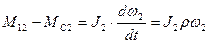
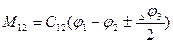 при
при 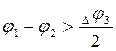 М12=0 при
М12=0 при 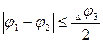
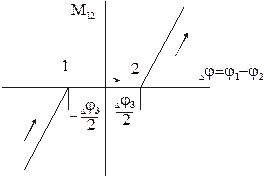 Во время пуска при разомкнутом зазоре механическая связь между инерционными массами J1 и J2 отсутствует и под действием момента двигателя М=М1 инерционные массы J1 движутся равноускоренно со скоростью
Во время пуска при разомкнутом зазоре механическая связь между инерционными массами J1 и J2 отсутствует и под действием момента двигателя М=М1 инерционные массы J1 движутся равноускоренно со скоростью
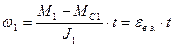 где
где
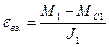 - ускорение при выборе зазора.
- ускорение при выборе зазора.
За время выбора зазора двигатель успевает разогнаться до некоторой начальной скорости wlнач и запасти кинетическую энергию 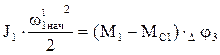 , откуда
, откуда
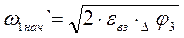 .
.
Это уравнение соответствует наиболее тяжелому случаю выбору полного зазора, когда начальное значение Dj соответствует точке 1 (см. зависимость 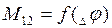 ), а заканчивается выбор зазора в т.2.
), а заканчивается выбор зазора в т.2.
После выбора зазора инерционная масса J2 будет оставаться еще неподвижной. Начнется деформация (закручивание) упругих элементов под действием момента М12.Это будет продолжаться до тех пор, пока М12, возрастая, не превысит МС2. За время нарастания М12 до МС2 скорость инерционной массы J1 дополнительно увеличивается до w1нач.. Т.к. инерционные массы механизма при этом неподвижны, процесс выбора зазора заканчивается упругим ударом, при котором запасенная во вращающихся с угловой скоростью w1нач. массах J1 кинетическая энергия 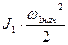 частично рассеивается в виде тепла, а в основном переходит в энергию упругих деформаций, вызывая дополнительные динамические нагрузки передач. Для их количественной оценки найдем зависимость
частично рассеивается в виде тепла, а в основном переходит в энергию упругих деформаций, вызывая дополнительные динамические нагрузки передач. Для их количественной оценки найдем зависимость 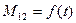 для 3-го этапа переходного процесса разгона, когда
для 3-го этапа переходного процесса разгона, когда 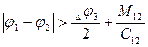 . Уравнения движения на этом этапе
. Уравнения движения на этом этапе 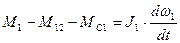 ;
; 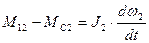 ;
; 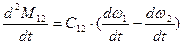 .
.
Умножая 1-е уравнение на 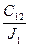 , 2-е на
, 2-е на 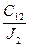 и вычитая из полученного 1-го полученное 2-е, а также имея в виду 3-е уравнение, получим
и вычитая из полученного 1-го полученное 2-е, а также имея в виду 3-е уравнение, получим 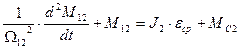 , где
, где
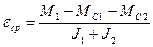 ;
; 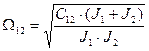 .
.
Правая часть полученного уравнения определяет частное решение. Общее решение уравнения с учетом частного решения 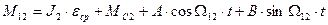
Постоянные А и В находятся из начальных условий. При t = 0 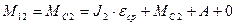 , откуда
, откуда 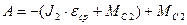 .
.
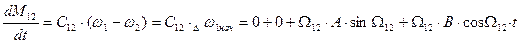
При t = 0 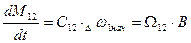 , откуда
, откуда 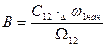
Т.о. 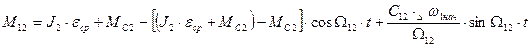 или
или
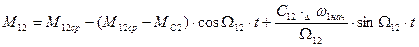
Здесь М12СР – момент нагрузки в передаче при отсутствие колебаний во время пуска, причем 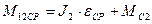 .
.
После преобразований получим
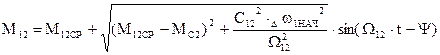 , где
, где 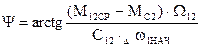
Максимум нагрузки в передачах будет при 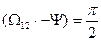
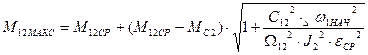 .
.
Это выражение получено путем умножения и деления 2-го слагаемого под корнем на 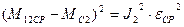
Анализ полученного выражения говорит о том, что за счет возникающих в результате удара после выбора зазора механических колебаний максимальная нагрузка передач возрастает по сравнению с нагрузкой М12СР, которая имела бы место при жесткой связи масс J1и J2 и отсутствии зазора. Отношение 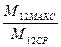 называется динамическим коэффициентом КДИН.
называется динамическим коэффициентом КДИН.
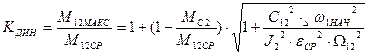 .
.
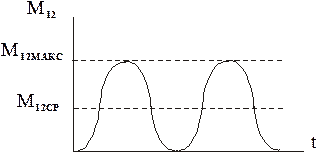 При пуске с предварительно выбранным зазором
При пуске с предварительно выбранным зазором 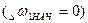 и МС2=0 КДИН=2, т.е. упругие колебания вдвое увеличивают рабочие нагрузки передач (см. график
и МС2=0 КДИН=2, т.е. упругие колебания вдвое увеличивают рабочие нагрузки передач (см. график 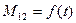 ), т.е.
), т.е. 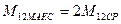 .
.
При наличии невыбранных зазоров ( 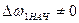 ) максимум нагрузки возрастает и может достичь опасных для прочности передач значений. Если в выражении для КДИН подставить Значения eСР и W12, обозначив
) максимум нагрузки возрастает и может достичь опасных для прочности передач значений. Если в выражении для КДИН подставить Значения eСР и W12, обозначив 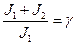 , можно записать:
, можно записать:
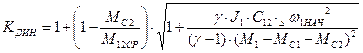 .
.
Отсюда видно, что КДИН тем больше, чем больше J1 и чем больше жесткость механической связи.
При 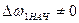 упругость передач является фактором, снижающим динамические ударные нагрузки. Поэтому при проектировании эл.привода необходимо предусматривать законы управления, обеспечивающие повышение плавности выбора зазоров и снижение ударных нагрузок до допустимых значений путем ограничения достигаемой при выборе зазоров скорости
упругость передач является фактором, снижающим динамические ударные нагрузки. Поэтому при проектировании эл.привода необходимо предусматривать законы управления, обеспечивающие повышение плавности выбора зазоров и снижение ударных нагрузок до допустимых значений путем ограничения достигаемой при выборе зазоров скорости 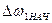 .
.
Динамические колебательные процессы, если исключить из рассмотрения низкочастотные колебания, обусловленные раскачиванием перемещаемых на гибких подвесках грузов, в среднем не влияют на длительность переходного процесса пуска, реверса, торможения эл.привода и не снижают производительность механизма. Однако, считаться с ними приходится, т.к. они сказываются на точности работы установки, бесполезно увеличивают нагрузку передач и рабочего оборудования и ускоряют их износ.
Дата добавления: 2015-01-19; просмотров: 1324;
