Передаточные функции, структурные схемы и частотные характеристики механической части электропривода как объекта управления.
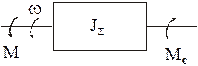 Сначала рассмотрим механическую часть как абсолютно жесткую механическую систему. Уравнение движения такой системы:
Сначала рассмотрим механическую часть как абсолютно жесткую механическую систему. Уравнение движения такой системы:
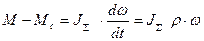
Передаточная функция 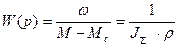
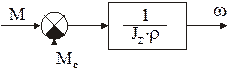 Структурная схема механической части в этом случае, как следует из уравнения движения, имеет вид, изображенный на рис.
Структурная схема механической части в этом случае, как следует из уравнения движения, имеет вид, изображенный на рис.
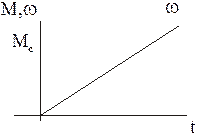
Изобразим ЛАЧХ и ЛФЧХ этой системы. Т.к. звено с передаточной функцией 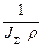 является интегрирующим, то наклон ЛАЧХ – 20 дб/дек. При приложении нагрузки Mc=const скорость в такой системе нарастает по линейному закону и если М=Мс не ограничить, то она возрастает до ¥. Сдвиг между колебаниями М и w, т.е. между выходной и входной величиной постоянен и равен
является интегрирующим, то наклон ЛАЧХ – 20 дб/дек. При приложении нагрузки Mc=const скорость в такой системе нарастает по линейному закону и если М=Мс не ограничить, то она возрастает до ¥. Сдвиг между колебаниями М и w, т.е. между выходной и входной величиной постоянен и равен 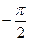 .
.
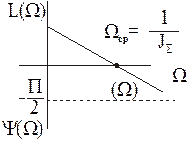 |  | ||
Расчетная схема двухмассовой упругой механической системы, как было показано ранее, имеет вид, изображенный на рис.
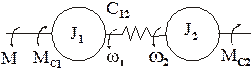 Структурная схема этой системы может быть получена на основе уравнений движения
Структурная схема этой системы может быть получена на основе уравнений движения 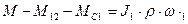 ;
; 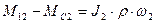 ;
; 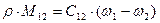
Передаточные функции 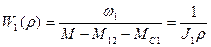
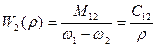
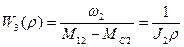 .
.

Структурная схема, соответствующая этим управлениям, имеет вид:
Для исследования свойств этой системы как объекта управления принимаем МС1=МС2=0 и выполним синтез по управляющему воздействию. Используя правила эквивалентного преобразования структурных схем, можно получить передаточную функцию 
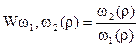 ,связывающую выходную координату w2 , с входной, которой является w1 и передаточную функцию
,связывающую выходную координату w2 , с входной, которой является w1 и передаточную функцию 
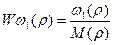 при выходной координате w1.
при выходной координате w1.
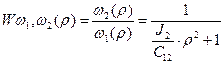 ;
; 

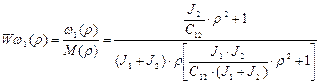
Характеристическое уравнение системы: 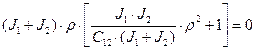 .
.
Корни уравнения: 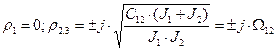 .
.
Здесь W12 – резонансная частота свободных колебаний системы.
Наличие мнимых корней свидетельствует о том, что система находится на грани устойчивости и если ее толкнуть, то она затухать не будет и на частоте W12 возникает резонансный пик.
Обозначив 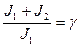 ;
; 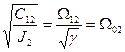 , где
, где
W02 – резонансная частота 2-й инерционной массы при J1 ®¥.
С учетом этого передаточные функции 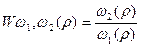 , и
, и 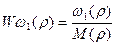 будут иметь вид:
будут иметь вид:
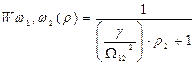 ;
; 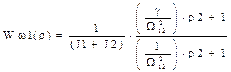
 |
Эти соотношения позволяют представить механическую часть эл.привода, как объекта управления в виде 3-х звеньев (см. рис.).
Из этой схемы следует, что передаточная функция системы по управляющему воздействию при выходной переменной w2, т.е. Ww2(r) равна: 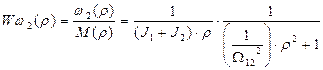 .
.

Ей соответствует структурная схема:
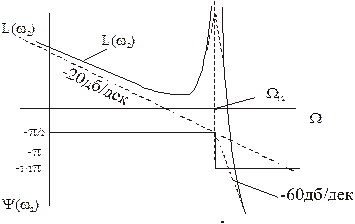 Для анализа поведения системы построим ЛАХЧ и ЛФЧХ механической части как объекта управления, сначала при выходной координате w2, заменив в выражении Ww2(r) R на jW. Они изображены на рис.
Для анализа поведения системы построим ЛАХЧ и ЛФЧХ механической части как объекта управления, сначала при выходной координате w2, заменив в выражении Ww2(r) R на jW. Они изображены на рис.
Из него следует, что в системе возникают механические колебания, причем число колебаний доходят до 10-30. При этом колебательность инерционной массы J2 выше, чем Массы J1. При W>W12 наклон высокочастотной асимптоты L(w2) равен – 60 дб./дек. И нет факторов, которые ослабляли бы развитие резонансных явлений при любом 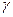 . Следовательно, когда важно получить требуемое качество движения инерционной массы J2, а также при регулировании координат системы, пренебрегать влиянием упругости механических связей без предварительной проверки нельзя.
. Следовательно, когда важно получить требуемое качество движения инерционной массы J2, а также при регулировании координат системы, пренебрегать влиянием упругости механических связей без предварительной проверки нельзя.
В реальных системах имеется естественное демпфирование колебаний, которое, правда существенно не сказывается на форме ЛАХЧ и ЛФЧХ, однако ограничивает резонансный пик конечным значением, как показано пунктиром на рис.
Для анализа поведения системы при выходной координате w1 также построим ЛАХЧ и ЛФХЧ механической части как объекта управления. Структурная схема, вытекающая из передаточной

функции 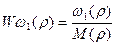 имеет вид:
имеет вид:
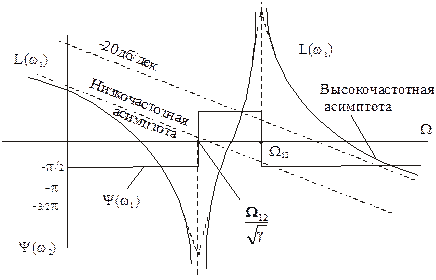 Частотные характеристики приведены ниже:
Частотные характеристики приведены ниже:
Движение инерционной массы J1, как следует из характеристики и структурной схемы, при небольших частотах колебаний упругого взаимодействия определяется суммарным моментом инерции 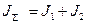 , причем механическая часть ведет себя как интегрирующее звено, т.к. характеристика L(w1) асимптотически приближается к асимптоте, имеющий наклон – 20 дб/дек. При M=const скорость w1 изменяется по линейному закону, на который накладываются колебания, обусловленные упругой связью. При приближении частоты колебаний момента М к W12 амплитуда колебаний скорости w1 возрастает и при W=W12 стремиться к бесконечности. Отсюда следует, что чем ближе
, причем механическая часть ведет себя как интегрирующее звено, т.к. характеристика L(w1) асимптотически приближается к асимптоте, имеющий наклон – 20 дб/дек. При M=const скорость w1 изменяется по линейному закону, на который накладываются колебания, обусловленные упругой связью. При приближении частоты колебаний момента М к W12 амплитуда колебаний скорости w1 возрастает и при W=W12 стремиться к бесконечности. Отсюда следует, что чем ближе 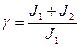 к 1, т.е. при J2<<J1, тем меньше сказывается влияние упругости на механическую часть системы. Поскольку обычно g=1,2¸1,6, влиянием упругости можно пренебречь и передаточную функцию
к 1, т.е. при J2<<J1, тем меньше сказывается влияние упругости на механическую часть системы. Поскольку обычно g=1,2¸1,6, влиянием упругости можно пренебречь и передаточную функцию 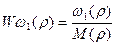 можно считать как функцию интегрирующего звена (в структурной схеме во втором звене числитель и знаменатель выражения сократятся)
можно считать как функцию интегрирующего звена (в структурной схеме во втором звене числитель и знаменатель выражения сократятся) 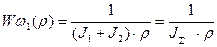 и механическую часть эл.привода можно рассматривать как абсолютно жесткое механическое звено.
и механическую часть эл.привода можно рассматривать как абсолютно жесткое механическое звено.
При g>>1, т.е. J2>J1 и если частота среза 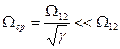 , механическую часть эл.привода также можно считать абсолютно жесткой (С12=бесконечности).
, механическую часть эл.привода также можно считать абсолютно жесткой (С12=бесконечности).
Как уже сказано выше, обычно g=1,2¸1,6, но вообще то g=1,2¸100. Величина 100 характерна для редукторных тихоходных электроприводов, например, для механизма поворота стрелы шагающего экскаватора с емкостью ковша 100м3 и длиной стрелы 100м.
Дата добавления: 2015-01-19; просмотров: 1306;
