Средняя гармоническая величина
Если по условиям задачи необходимо, чтобы неизменной оставалась при осреднении сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней. Иными словами, если неизвестен знаменатель в определении средней величины, то используют формулу средней гармонической.
Формула гармонической средней такова:
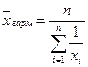 - простая (для негруппированных данных)
- простая (для негруппированных данных)
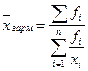 - взвешенная (для группированных данных)
- взвешенная (для группированных данных)
Например, автомобиль с грузом от предприятия до склада доехал со скоростью 40 км/ч, а обратно порожняком - со скоростью 60 км/ч. какова средняя скорость автомобиля за обе поездки? Пусть расстояние перевозки составило s км. Никакой роли при расчете средней величины расстояние s не имеет. Здесь главное, чтобы при замене скоростей х1 = 60 км/ч и х2 = 40 км/ч на среднюю величину необходимо, чтобы неизменным оставалось время, затраченное на обе поездки, иначе средняя скорость может оказаться любой.
Время поездок есть s/x1 + s/x2. Итак, имеем s/ 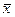 + s/
+ s/ 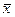 = s/x1 + s/x2. Сократив все члены равенства на s, получим 1/
= s/x1 + s/x2. Сократив все члены равенства на s, получим 1/ 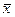 + 1/
+ 1/ 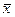 = 1/x1 + 1/x2, т.е. выполняется условие гармонической средней. Подставляя известные значения, получаем:
= 1/x1 + 1/x2, т.е. выполняется условие гармонической средней. Подставляя известные значения, получаем:
2/ 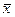 = 1/60 + 1/40, x = 2 / (1/60 + 1/40) = 2 ∙ 120 / 5 = 48 км/x
= 1/60 + 1/40, x = 2 / (1/60 + 1/40) = 2 ∙ 120 / 5 = 48 км/x
Арифметическая средняя 50 км/ч неверна, так как приводит к другому времени движения, чем на самом деле. Если расстояние равно, например, 96 км, то реальное время составит: 96/60 + 96/40 = 1,6 + 2,4 = 4 ч.
То же время дает гармоническая средняя: (96 ∙ 2) / 48 = 4 ч.
Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних. Различаются они лишь показателем. Степенная средняя степени k есть корень k-той степени из частного от деления суммы индивидуальных значений признака в к-й степени на число индивидуальных значений:
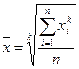
При к=1 получаем арифметическую среднюю, при к=2 - квадратическую среднюю, прик=3 - кубическую, при к=0 - геометрическую, при к= -1 - гармоническую. Чем выше показатель степени к, тем больше значение средней величины. Если все исходные значения признака равны, то все средние равны этой константе. Итак, имеем следующее соотношение, которое называется правилом мажорантности средних:
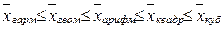
Посмотрим, как работает это правило на примере.
Допустим , студент получил в сессию две оценки 2 и 5. Каков его средний балл?
Если судит по средней арифметической, то средний балл равен 3,5. Но если вычислить среднюю гармоническую, то она уже будет равна
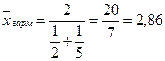
и студент остается в среднем двоечником, не дотянувшим до тройки. Однако, если мы вычислим среднюю кубическую величину, то получим:
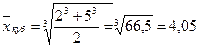
И студент уже выглядит хорошистом. И только если студент провалил оба экзамена, статистика помочь уже не сможет.
Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Главное требование к формулам расчета среднего значения состоит в том, чтобы все этапы расчета имели реальное содержание: полученное среднее значение может заменить все индивидуальные значения признака без нарушения связи индивидуального и сводного показателя. Итоговый сводный показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины. При выборе показателя используют следующее правило: определяют три взаимосвязанных показателя, включая и тот, по которому требуется рассчитать среднее значение. Если имеются первичные данные по двум каким-либо показателям из этого списка, то отсутствующий третий и будет определяющим. Если имеются данные по всем трем, то исследователь вправе использовать формулу как средней арифметической , так и средней гармонической, результат должен совпасть.
Покажем применение этого правила на примере. Пусть известны цены товара одного и того же наименования по каждому из n торговых заведений. Требуется определить общую среднюю цену товара. Обозначим индивидуальные уровни цен как р1, р2, …, рn, а среднюю цену как 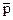 . В качестве итогового сводного показателя выберем общую сумму фактической выручки от реализации V. Тогда
. В качестве итогового сводного показателя выберем общую сумму фактической выручки от реализации V. Тогда 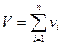 , где vi – объем выручки, полученный от реализации товара по каждой отдельной торговой точке. Так как для каждого торгового заведения объем реализации равен произведению цены рi на количество фактически проданного товара в натуральном выражении (qi), то получаем:
, где vi – объем выручки, полученный от реализации товара по каждой отдельной торговой точке. Так как для каждого торгового заведения объем реализации равен произведению цены рi на количество фактически проданного товара в натуральном выражении (qi), то получаем:
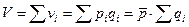
В этом выражении индивидуальные значения цены заменены общим средним уровнем цены. Следовательно из последнего уравнения имеем:
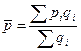
В числителе – суммарный объем реализации в денежном выражении по всем торговым точкам, а в знаменателе – общий объем реализации продукции в натуральном выражении. Полученное выражение – формула средней арифметической взвешенной.
Если в качестве определяющего показателя взять общий объем реализации в натуральном выражении, то получаем:
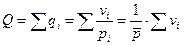
Следовательно, 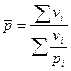 , где vi – объем реализации, полученный каждой торговой точкой.
, где vi – объем реализации, полученный каждой торговой точкой.
Таким образом, если кроме индивидуальных значений признака (в нашем случае индивидуальные цены) имеются данные о фактических объемах реализации в стоимостном выражении, то расчет проводят по формуле средней гармонической взвешенной.
В нашем примере можно выделить три взаимосвязанных показателя:
- объем выручки от реализации товара (руб.);
- реализация продукции (шт.);
- цена (руб./шт.).
В 1-м случае предполагалось, что не указан объем реализации в денежном выражении, но известны данные по объему продаж (qi, шт) и ценам (рi, руб/шт), что привело к формуле средней арифметической взвешенной. Во втором случае предполагалось, что отсутствуют данные о реализации продукции в натуральном выражении – в итоге получили формулу средней гармонической.
Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних. Различаются они лишь показателем. Степенная средняя степени k есть корень к-той степени из частного от деления суммы индивидуальных значений признака в к-й степени на число индивидуальных значений:
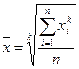
Все виды средних можно представить в следующей таблице:
| Значение k | Наименование средней | Формула | |
| простая | взвешенная | ||
| -1 | гармоническая | 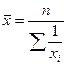
| 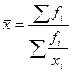
|
| ® 0 | геометрическая | 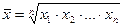
| 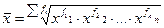
|
| арифметическая | 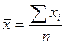
| 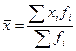
| |
| квадратическая | 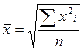
| 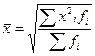
|
Дата добавления: 2015-03-03; просмотров: 1708;
