Структурные характеристики вариационного ряда. Показатели размера и интенсивности вариации.

При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, строение. К ним относят медиану и моду, которые еще часто называют структурными средними вариационного ряда.

Медиана распределения. Медиана - величина варьирующего признака, делящая совокупность на две равные части - со значениями признака меньше медианы и со значениями признака больше медианы. При нечетном количестве единиц за медиану берут среднюю единицу. При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при десяти значениях признака - среднюю из пятого и шестого значений в ранжированном ряду.

В интервальном вариационном ряду для нахождения медианы применяется формула

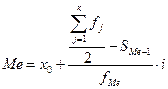
Где Ме - медиана;

х₀ - нижняя граница интервала, в котором находится медиана;

S_Me-1 - накопленная частота в интервале, предшествующем медианному;

f_Me - частота в медианном интервале;

i - величина медианного интервала;

к - число групп

В нашей таблице по урожайности с/х предприятий медианным является среднее из 143 значений, т.е. 72 от начала ряда значений урожайности. Как видно из ряда накопленных частот, оно находится в 4 интервале. Тогда

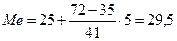ц/га

При нечетном числе единиц совокупности номер медианы, как видим, равен не ∑f_i : 2, как в формуле, а (∑f_i +1) : 2, но это различие несущественно и обычно игнорируется на практике. В дискретном ряду вариационном ряду медианой следует считать значение признака в той группе, в которой накопленная частота превышает половину численности совокупности.

Квартили распределения. Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные части. Их называют квартилями и обозначают заглавной буквой Q с номером квартили. Ясно, что Q₂ совпадает с Ме. Для первого и третьего квартилей приводим формулу и расчет по данным таблицы урожайности:

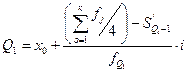
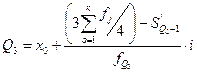
Где Q₁ - первая квартиль;

х₀ - нижняя граница интервала, в котором находится первая квартиль;

f ^'_Q1-1 - накопленная частота в интервале, предшествующем квартильному;

f_Q1 - частота в квартильном интервале;

i - величина квартильного интервала;

к - число групп

Аналогично определяется третья квартиль (в формуле вместо Q₁ пишем Q₃)

В нашем примере Q₁ = 25 + (35,75 -35) : 41 ∙ 5 = 25,09 ц/га

Q₃ = 35+ (107,25 - 102) : 21 ∙ 5 36,25 ц/га

Мода распределения. Очень большое значение для изучения вариации является мода - это такая величина признака, которая встречается в изучаемом ряду чаще всего, обозначают Мо. В дискретном ряду мода определяется без вычислений как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных значений модального признака имеются в вариационном ряду, он считается бимодальным или мультимодальным. Это говорит о неоднородности совокупности, возможно, она представляет собой слияние нескольких совокупностей с разными модами.

В интервальном вариационном ряду модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящейся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой. Такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу:

где х₀ - нижняя граница модального интервала;

f_Mo - частота в модальном интервале

f_Mo-1 - частота в предыдущем интервале;

f_Mo+1 - частота в интервале, следующем за модальным;

i - величина модального интервала.

Открываем таблицу с урожайностью и рассчитываем моду. Наибольшая частота - 41 и находится в 4 интервале. Нижняя граница этого интервала 25. Имеем: Мо = 25 + (41-20) / (41-20) + (41-26) * 5 = 27,9 ц/га.

Вычисление моды в интервальном ряду весьма условно. Приближенно Мо может быть определена графически.