Закономерности распределения.

В приведенном примере можно заметить определенную зависимость между изменением варьирующегося признака и частот. Частоты в этих рядах с увеличением значения признака первоначально увеличиваются, а затем по достижении какой-то максимальной величины в середине ряда уменьшаются. Это свидетельствует о том, что частоты в вариационных рядах изменяются закономерно в связи с изменением варьирующегося признака. Такое изменение частот в вариационных рядах называются закономерностями распределения. Как и статистические закономерности, закономерности распределения наиболее отчетливо проявляются только при массовом наблюдении.

Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот в вариационном ряду. Различают следующие разновидности кривых распределения:

· одновершинные кривые: симметричные, умеренно асимметричные и крайне асимметричные;

· многовершинные кривые.

Для однородных совокупностей характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп.

Для изучения распределения используют показатели, которые получили название центральных моментов распределения порядка, соответствующего степени, в которую возводят отклонения отдельных величин от средней величины. Запишем все формулы в таблице.

Порядок момента	Формула
по несгруппированным данным	по сгруппированным данным
первый ( )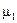
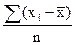
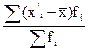
второй (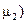
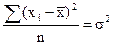
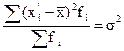
третий (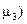
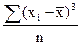
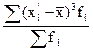
четвертый (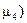

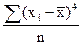
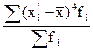
На основе момента третьего порядка строят показатель, характеризующий степень асимметрии распределения, его называют коэффициентом асимметрии:

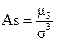
Величина показателя асимметрии может быть положительной и отрицательной

При As>0 правосторонняя асимметрия (правая ветвь относительно максимальной ординаты вытянута больше, чем левая). При правосторонней асимметрии между показателями вариации существует соотношение: М₀<М_е< 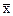_. При As<0 - левосторонняя асимметрия.

Между показателями в этом случае имеется следующее соотношение: М₀>М_е> _.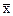

Английский статистик К. Пирсон на основе разности между средней величиной и модой предложил другой показатель асимметрии:

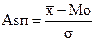
Показатель асимметрии Пирсона зависит от степени асимметрии в средней части ряда, а показатель асимметрии, основанный на моменте третьего порядка - от крайних значений признака.

С помощью момента четвертого порядка характеризуются еще более сложное свойство рядов распределения, чем асимметрия, называемое эксцессом. Показатель эксцесса:

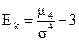
Часто эксцесс интерпретируется как "крутизна" распределения.

При Е_к>0, получаем островершинное распределение, при Е_к<0 - плосковершинное.

Хотя показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако их определение имеет не только описательное значение. Часто асимметрия и эксцесс дают определённые указания для дальнейшего исследования социально-экономических явлений. Например, появление значительного отрицательного эксцесса указывает на качественную неоднородность исследуемой совокупности.