Закономерности

После того как мы познакомились с различными видами и формами средних величин, включая и неявную их форму, можно перейти к понятию о средних. В широком понимании термина средней величиной является всякий обобщающий показатель, характеризующий обобщенное значение признака, связи признаков, их динамики и структуры в совокупности массовых явлений.

Так, средними в широком смысле слова являются такие показатели, как доля мужчин в общем числе жителей страны (ведь эта доля разная в разных регионах), плотность населения, коэффициент смертности, ожидаемая продолжительность жизни родившихся в данном году и др. Рассматриваемые далее в этой главе показатели вариации признака в совокупности, а также в главе 8 показатели корреляционной связи тоже средние в широком смысле слова, так как измеряют среднее различие между значениями одного признака у разных единиц совокупности или среднюю связь вариации одного признака с вариацией другого.

В такой же степени средними являются и показатели темпов роста продукции промышленности или национального дохода страны, обобщающие темпы разных отраслей и регионов; средними являются меры .колеблемости урожайности за ряд лет (гл. 9), обобщающие влияние на урожайность разных лет метеорологических и экономических условий производства.

Понятие средней в широком смысле слова сближается с такой философской категорией, как закон («закон есть общее в явлениях»), закономерность. Это далеко не случайное родство. Рассмотрим , сущность процесса осреднения на примере арифметической средней согласно формуле (5.1). Среднюю считаем типической, определенной по однородной совокупности. Однородность индивидуальных значений признака — это проявление их общих свойств, обусловленных основными условиями и закономерностями массового процесса, порождающего данную совокупность. Однако кроме общих условий, кроме закономерности на каждую единицу совокупности влияют индивидуальные, особенные условия, случайные события, не связанные причинно с общей закономерностью. Поэтому можно индивидуальные значения признака х, представить как состоящие из элемента, обусловленного общей закономерностью для всех единиц совокупности (обозначим этот элемент с), так и элемента ∆_i, индивидуального для каждой единицы совокупности. Итак, х_i = с + ∆_i, где ∆_i может быть как положительной, так и отрицательной величиной, как малой, так и большой величиной в сравнении е c.

Теперь вычислим среднее значение признака для совокупности из п единиц:

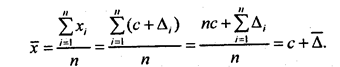
Итак, средняя величина признака слагается из элемента, выражающего закономерность, общую для всей совокупности, и из средней величины элементов, отражающих индивидуальные условия отдельных единиц этой совокупности. Элементы Д, могут иметь положительные и отрицательные, большие и малые значения. При осреднении они согласно закону больших чисел взаимопогащаются в зависимости от объема совокупности: тем в большей мере, чем больше объем совокупности п. Об этом говорит формулировка закона больших чисел, данная великим русским математиком П. Л. Чебышевым (1821-1894). Чем больше объем однородной совокупности, тем полнее взаимопогашение случайных (по отношению к совокупности в целом и ее законам) элементов признака х; полнее и надежнее, с большей вероятностью среднее значение признака измеряет действие общих для совокупности закономерностей.

Однако случайная вариация индивидуальных величин признаков - это не только некоторая помеха, туман, «шум» в информационном смысле, затрудняющий познание закономерности. Вариация - неотъемлемая, необходимая черта, свойство массовых явлений, имеющее громадное самостоятельное значение в развитии природы и общества.

Создатель учения о средних величинах бельгийский статистик А, Кегле по этому поводу писал следующее: «В мире существует общий закон, предназначенный как бы для того, чтобы разливать жизнь во Вселенной; в силу этого закона все живущее подлежит бесконечному разнообразию... Каждый предмет подвержен флюктуациям»[4].

В следующих разделах данной главы переходим к методам статистического изучения этого «общего закона Вселенной» - вариации массовых явлений и их признаков.