Соотношение между формами средних величин

Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних. Различаются они лишь показателем. Степенная средняя степени k есть корень k-й степени из частного от деления суммы индивидуальных значений признака в k-й степени на число индивидуальных значений:

При k = 1 получаем арифметическую среднюю, при k -2 - квад-рагическую, при k = 3 - кубическую, при k = 0 - геометрическую, при k = -1 — гармоническую среднюю. Чем выше показатель степени k, тем больше значение средней величины (если индивидуальные значения признака варьируют). Если все исходные значения признака равны, то и все средние равны этой константе. Итак, имеем следующее соотношение, которое называется правилом мажорантности средних:

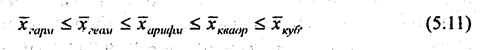
Пользуясь этим правилом, статистика может в зависимости от настроения и желания ее «знатока» либо «утопить», либо «выручить» студента, получившего на сессии оценки 2 и 5. Каков его средний балл?

Если судить по средней арифметической, то средний балл равен 3,5. Но если декан желает «утопить» несчастного и вычислит среднюю гармоническую

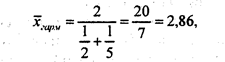
то студент остается в среднем двоечником, не дотянувшим до тройки. Однако студенческий комитет может возразить декану и представить среднюю кубическую величину:

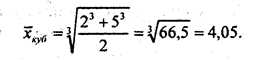
Студент уже выглядит «хорошистом» и даже претендует на стипендию! И только в том случае, если лентяй провалил оба экзамена, статистика помочь не в состоянии: увы, все средние из двух двоек равны все той же двойке!