Средняя геометрическая величина. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину. Ее формула такова:

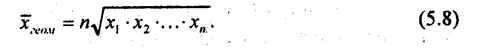
Основное применение геометрическая средняя находит при определении средних темпов роста, о чем сказано в главе 9. Пусть, например, в результате инфляции за первый год цена товара возросла в 2 раза к предыдущему году, а за второй год еще в 3 раза к уровню предыдущего года. Ясно, что за два года цена выросла в 6 раз. Каков средний темп роста цены за год? Арифметическая средняя здесь непригодна, ибо если за год цены возросли бы в 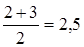раза, то за два года цена возросла бы в 2,5×2,5 = 6, 25 раза, а не в 6 раз. Геометрическая средняя дает правильный ответ: 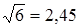раза.

Геометрическая средняя величина дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака. Например, если максимальный размер выигрыша в лотерее составляет миллион рублей, а минимальный - сто рублей, то какую величину выигрыша можно считать средней между миллионом и сотней? Арифметическая средняя явно непригодна, она составляет 500 050 руб., а это, как и миллион, крупный, никак не средний выигрыш; он качественно однороден с максимальным и резко отличен от минимального. Не дают верного ответа ни квадратическая средняя (707 107 руб.), ни кубическая (793 699 руб.), ни рассматриваемая далее гармоническая средняя (199,98 руб.), слишком близкая к минимальному значению. Только геометрическая средняя дает верный с точки зрения экономики и логики ответ: руб. Десять тысяч — не миллион, и не сотня! Это, действительно, нечто среднее между ними.