Применение простой и взвешенной средней

Простая и взвешенная средние величины различаются не только по величине (не всегда), по способу вычисления, но и по своей роли в решении различных задач статистического анализа. Рассмотрим, например, среднюю величину урожайности картофеля в группе хозяйств. Если эта средняя при решении поставленной задачи входит в систему показателей площади посадки, валового сбора, себестоимости, суммы затрат и других характеристик производства, то следует применять взвешенную среднюю, так как произведение невзвешенной средней на общую сумму площадей не даст суммы валового сбора.

Если же нас интересуют такие задачи, как измерение вариации урожайности между хозяйствами или связь урожайности с дозой органических удобрений, то следует применять простую среднюю величину урожайности, полностью абстрагируясь от размеров площадей посадки. Иначе на полученный результат повлияют различия площадей, совершенно не касающиеся этого признака. Точно так же, если необходимо изучить колебания урожайности за ряд лет и выявить их связь с температурой июня и суммой осадков за лето, нужно применять простую среднюю урожайность за ряд лет, абстрагируясь от различия размеров площадей в разные годы.

Чтобы правильно применять средние величины, следует знать, от каких причин зависит различие между простой и взвешенной средними. Рассмотрим этот вопрос на примере арифметической средней. Пусть x̅ - простая средняя, х̅_z - взвешенная средняя, в которой весами выступают значения признака z, п - число единиц совокупности. Отклонения индивидуальных значений признака х_i от простой средней х̅ обозначим ∆_xi = х_i - х̅. Отклонения признака веса ∆_zi = z_i -z̅. Тогда индивидуальные значения признаков х и z можно выразить через их средние и отклонения: х_i = х̅ + ∆_xi; z_i = z̅ + ∆_zi, а взвешенную среднюю х, представить в виде

Перемножим величины в скобках и просуммируем почленно, имея в виду, что 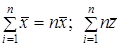. Средние величины можно вынести за знак суммирования, как константы. Получим:

Так как суммы отклонений индивидуальных значений признака от средней арифметической согласно первому ее свойству равны нулю, то второе и третье слагаемые числителя также равны нулю.

Остается:

Числитель второго слагаемого в формуле (5.4) - это числитель коэффициента корреляции между осредняемым и весовым признаками (см. формулы 8.11 и 8.14). Подставив выражение коэффициента корреляции /^ в (5.4), получим:

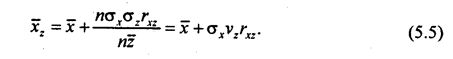
Итак, средняя арифметическая взвешенная равна простой средней плюс произведение среднего квадратического отклонения ос-редняемого признака на коэффициент вариации весового признака и на коэффициент корреляции между этими признаками. Если обе части равенства (5.5) разделить на простую среднюю х, получим:

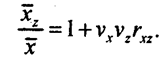
(О среднем квадратическом отклонении и коэффициенте вариации см. ниже в этой главе.)

Из (5.5) следует, что взвешенная средняя равна простойв трех случаях:

• а) если не варьирует изучаемый признак, σ_х = 0 - тривиальная ситуация, когда и сами средние не нужны;

• б) при условии, что не варьирует признак-вес v_z = 0;

• в) в случаях, когда между осредняемым и признаком-весом нет линейной корреляции, r_xz = 0.

Взвешенная средняя больше простой, если эта корреляция прямая. Взвешенная средняя меньше простой средней, если эта корреляция обратная.