А. Равенство взвешенной и простой средних при сильной вариации весов.
В табл. 10.1 представлены данные примера А.
Таблица 10.1
| № товара | Цены | Индекс ip | Доля в базисной выручке d0 | ip· d0 | Вариаця долей | ||
| Р0 | Р1 | (dj0 – d0) | (dj0 – d0)2 | ||||
| 1,1 | 0,40 | 0,44 | 0,20 | 0,0400 | |||
| 2,0 | 0,25 | 0,50 | 0,05 | 0,0025 | |||
| 1,4 | 0,15 | 0,21 | -0,05 | 0,0025 | |||
| 1,6 | 0,10 | 0,16 | -0,10 | 0,0100 | |||
| 0,9 | 0,10 | 0,09 | -0,10 | 0,0100 | |||
| Итого | 1,4 | 1,00 | 1,40 | 0,0650 |
Невзвешенный средний индекс цен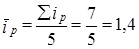 
Среднее значение веса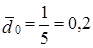 
Взвешенный средний индекс цен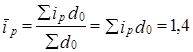 
Результат совпадает с простой средней. Между тем вариация весов значительна, стандартное отклонение
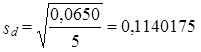
Коэффициент вариации весов
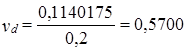,т.е. 57%.
Дата добавления: 2015-01-21; просмотров: 1458;