Абсолютные средние размеры вариации

Следующим этапом изучения вариации признака в совокупности является измерение характеристик силы, величины вариации. Простейшим из них может служить размах или амплитуда вариации -абсолютная разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений. Таким образом, размах вариации вычисляется по формуле

Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности. Предназначенный для данной цели показатель должен учитывать и обобщать все различия значений признака в совокупности без исключения. Число таких различий равно числу сочетаний по два из всех единиц совокупности; по данным табл. 5.6 оно составит: С^ = 10 153. Однако нет необходимости рассматривать, вычислять и осреднять все отклонения. Проще использовать среднюю из отклонений отдельных значений признака от среднего арифметического значения признака, а таковых всего 143. Но среднее отклонение значений признака от средней арифметической величины согласно известному свойству последней равно нулю. Поэтому показателем силы вариации выступает не алгебраическая средняя отклонений, а средний модуль отклонений:

По данным табл. 5.6 средний модуль, или среднее линейное отклонение, по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины, т.е. по формуле

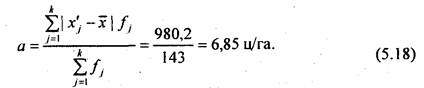
Это означает, что в среднем урожайность в изучаемой совокупности хозяйств отклонялась от средней урожайности по области на 6,85 ц/га. Простота расчета и интерпретации составляют положительные стороны данного показателя, однако математические свойства модулей «плохие»:их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является не средний модуль отклонений, а среднее квадратическое отклонение (в англоязычных программах для ЭВМ называемое «the standard deviation», сокращенно «s.d.» или просто «s», в русскоязычных - СКО). В статистической литературе среднее квадратическое отклонение от средней величины принято обозначать малой (строчной) греческой буквой сигма (ст) или s (см. гл. 7):

для ранжированного ряда

для интервального ряда

По данным табл. 5.6 среднее квадратическое отклонение урожайности зерновых составило:

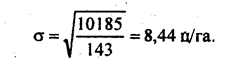
Следует указать, что некоторое округление средней величины и середин интервалов, например до целых, мало отражается на величине σ, которая составила бы при этом 8,55 ц/га.

Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений. Соотношение (у : а зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными с основной массой элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения σ : а = 1,2.