Мода распределения
Бесспорно, важное значение имеет такая величина признака, которая встречается в изучаемом ряду, в совокупности чаще всего. Такую величину принято называть модой и обозначать Мо. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Например, по данным табл. 5.1 чаще всего за футбольный матч было забито 2 мяча - 71 раз. Модой является число 2. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но больших, чем соседние) значений признака имеются в вариационном ряду, он считается соответственно бимодальным («верблюдообразным») либо мультимодальным. Это говорит о неоднородности совокупности, возможно, представляющей собой агрегат нескольких совокупностей с разными модами.
Так и в толпе туристов, приехавших из разных стран, вместо одной, преобладающей среди местных жителей модной одежды можно встретить смесь разных «мод», принятых у разных народов мира.
В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой.. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу (5.15):
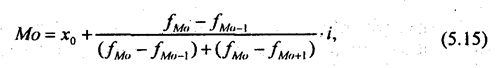
где x0 - нижняя граница модального интервала;
fMo - частота в модальном интервале;
fMo-1 - частота в предыдущем интервале;
fMo+1 - частота в следующем интервале за модальным;
i - величина интервала.
По данным табл. 5.6 рассчитаем моду:

Вычисление моды в интервальном ряду весьма условно. Приближенно Мо может быть определена графически (см. рис. 5.1).
К изучению структуры вариационного ряда средняя арифметическая величина тоже имеет отношение, хотя основное значение этого обобщающего показателя другое. В ряду распределения хозяйств по урожайности (табл. 5.6) средняя величина урожайности вычисляется как взвешенная по частоте середина интервалов х (по формуле (5.2)):
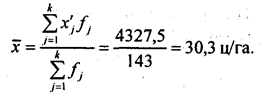
Соотношение между средней величиной, медианой и модой
Различие между средней арифметической величиной, медианой и модой в данном распределении невелико. Если распределение по форме близко к нормальному закону, то медиана находится между , модой и средней величиной, причем ближе к средней, чем к моде.
При правосторонней асимметриих̅ > Me > Mo;
при левосторонней асимметрии х̅ < Me < Mo.
Для умеренно асимметричных распределений справедливо равенство:
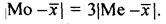
Дата добавления: 2015-01-21; просмотров: 1295;
