Асимметрия распределения и эксцесс

Асимметрия распределения означает, что частоты каких-либо двух вариантов, равноудаленных от центра распределения, не равны между собой. Графически асимметрия выражается различной длиной правой или левой ветви относительно максимальной ординаты. При асимметрии распределения значения средней арифметической, моды и медианы не совпадают.

Степень асимметрии определяется с помощью, например,

1) коэффициента асимметрии;

2) показателя асимметрии Пирсона.

Коэффициент асимметрии находится по формуле:

,

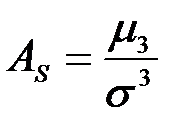где 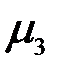- центральный момент третьего порядка, т.е.

.

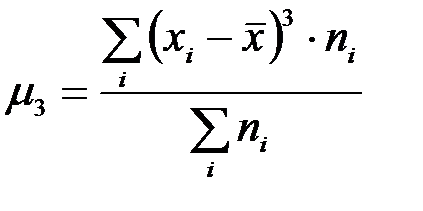Этот коэффициент характеризует асимметричность распределения крайних значений признака.

Показатель асимметрии Пирсона находится по формуле:

.

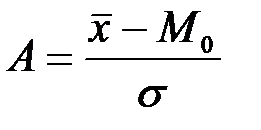Показатель асимметрии Пирсона характеризует асимметричность распределения в средней части ряда.

Эксцесс характеризует степень островершинности эмпирической кривой относительно кривой нормального распределения.

Коэффициент эксцессанаходится по формуле:

,

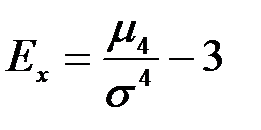где 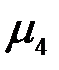- центральный момент четвертого порядка, т.е.

.

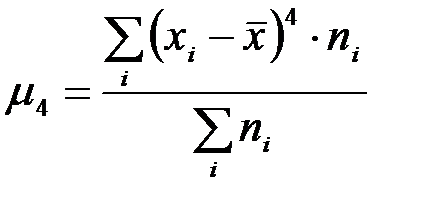Если получим 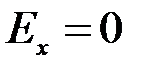, то вершины эмпирического и теоретического распределения совпадают. Если 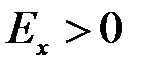, то эмпирическая величина выше вершины соответствующего теоретического распределения, а если 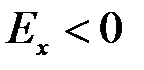, то эмпирическая вершина ниже вершины соответствующего теоретического распределения.