Пример 1.4

Рассмотрим расчет показателей асимметрии и эксцесса по данным табл. 1.1. Воспользуемся найденным выше средним значением объема вы-

полненных строительных работ одним предприятием 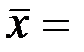670 млн. руб., среднеквадратическим отклонением 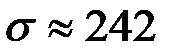млн. руб., модальным значение объема выполненных строительных работ 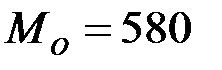млн. руб.

Таблица 1.6

Группы предприятий		Расчетные показатели
по объему выполненных	Число	центральное
работ (закрытые	предприя-	значение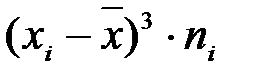
интервалы), млн. руб.	тий (n 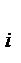)	интервала
		( )
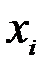300-500			-157464000
500-700			-4116000
700-1000
1000-1300
Итого:		—

Центральный момент третьего порядка:

.

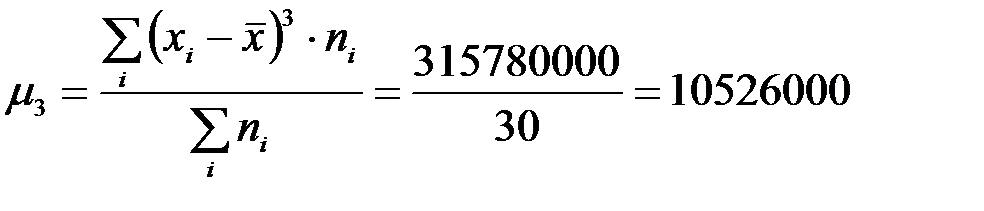Коэффициент асимметрии:

.

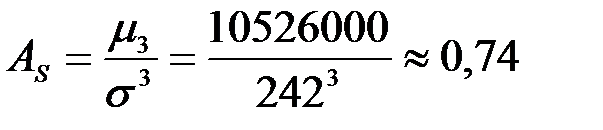Показатель асимметрии Пирсона:

.

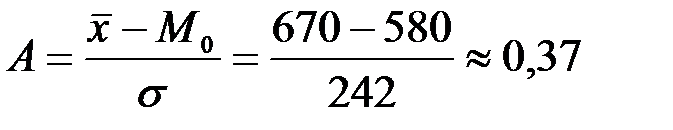Таким образом, данное распределение имеет правостороннюю асимметрию, причем в крайних значениях признака асимметрия более значительная, чем в средней части распределения.

Центральный момент четвертого порядка:

.

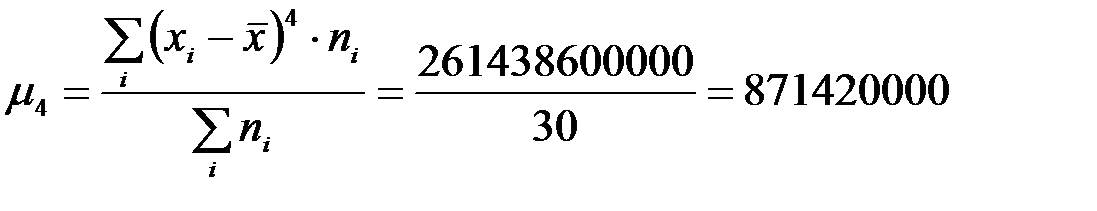Коэффициент эксцесса:

.

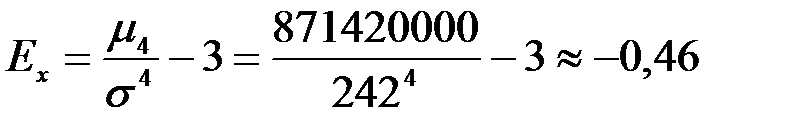Таким образом, вершина данного распределения ниже вершины соответствующего теоретического нормального распределения.