Б. Неравенство взвешенной и простой средних при слабой вариации весов.
В табл. 10.2 представлены данные примера Б.
Таблица 10.2
| № товара | Цены | Индекс ip | Доля, в базисной выручке d0 | ip· d0 | Вариация долей | ||
| Р0 | Р1 | (dj0 – d0) | (dj0 – d0)2 | ||||
| 1,1 | 0,15 | 0,165 | -0,05 | 0,0025 | |||
| 2,0 | 0,26 | 0,520 | 0,06 | 0.0036 | |||
| 1,4 | 0,19 | 0,266 | -0,01 | 0,0001 | |||
| .4 | 1,6 | 0,25 | 0,400 | 0,05 | 0,0025 | ||
| 0,9 | 0,15 | 0,135 | -0,05 | 0,0025 | |||
| Итого | X | X | 1,4 | 1,00 | 1,486 | 0,0112 |
невзвешенный средний индекс цен: 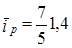
взвешенный средний индекс цен 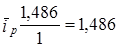 ;
;
вариация весов 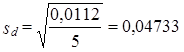
vd = 0,2366 или 23,7%, т. е. вариация весов намного слабее, чем в примере А.
Рассмотрим, в чем секрет таких соотношений? Обратимся к формуле взвешенной средней:
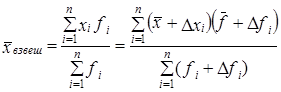
где x̅, f̅ - простые средние;
Dх, Df - отклонения от них.
Представим последнее выражение как:
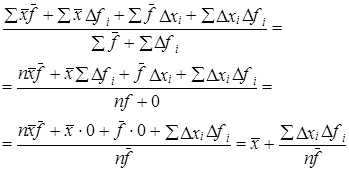
Числитель второго слагаемого можно представить через коэффициент корреляции между х и f:
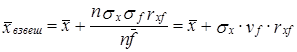 (10.3)
(10.3)
Эта формула аналогична формуле (5.6). Следовательно, средняя взвешенная равна простой средней, если:
• вариация признака х, отсутствует, т. е. sx = 0;
• вариация -весов fi отсутствует, т. е. vf = 0;
• нет корреляции между вариациями признака и весов, т. е. rxf = 0 (хотя бы сами х, и f, варьировали как угодно сильно).
Отношение взвешенной средней и простой можно выразить следующим образом:
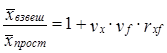 (10.4)
(10.4)
Поскольку различие взвешенной и простой средних зависит от корреляции значений признака и веса, постольку оно может оказаться большим при слабой вариации весов, чем при их сильной вариации (см. главу 5).
Рассмотрим соотношения между индексами (10.1) и (10.2) на примере табл. 10.3.
Таблица 10.3
Дата добавления: 2015-01-21; просмотров: 1715;
