Агрегатные индексы. Система индексов
Мы познакомились с построением сводных индексов на основе индивидуальных. Однако возможен и другой путь. Обратимся к формулам индексов Ласпейреса (10.5) и Пааше (10.7). Эти индексы могут быть рассчитаны на основе данных о количестве проданных товаров в базисном и отчетном периоде (по каждому j-му товару) q0j и q1j и ценах – р1j и р0j. Такие индексы принято называть агрегатными. Так же можно построить и Iq не через осреднение индивидуальных индексов, а на основе сравнения двух сумм (агрегатов), см. (10.7).
Агрегатные индексы считаются основной формой индексов. Они выполняют две функции:синтетическую и аналитическую. Первая функция обеспечивается тем, что в одном индексе обобщаются (синтезируются) непосредственно несоизмеримые явления. Например, цены на разные товары или разные товары, абсолютно не сопоставимые между собой в натуральном выражении. Когда мы записываем
,
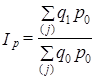то благодаря использованию ценового соизмерителя можно агрегировать данные по различным товарам.
Вторая функция - аналитическая - следует из взаимосвязи индексов. Дело в том, что практически каждый индекс можно рассматривать как составляющую некоей системы индексов, в которой его роль сводится к измерению одного из факторов общего изменения сложного явления и вклада этого фактора в совокупное изменение. Так, например, индекс цен можно рассматривать как показатель влияния изменения цен на выручку от продажи. Такая трактовка опирается на следующую связь признаков:
количество ´ цена = выручка (или затраты на покупку), т. е.
qp = w. (10.9)
Системе признаков соответствует система индексов (т. е. показателей их изменений). Исходя из этого можно записать:
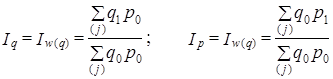(10.10)
Обратите внимание: эта запись соответствует трактовке индекса как метода анализа. Когда мы указываем Iw(q) или Iw(p) то имеем в виду измерение общего изменения результативного явления (в данном случае w) за счет одного из факторов (q или р). Конечно, можно ограничиться записью Iq и ip - ничего не изменится по существу.
При построении агрегатных индексов удобно пользоваться такими понятиями, как «индексируемый признак» и «признак-вес». Индексируемый - это признак, изменение которого характеризует данный индекс. Например, в Iq - это q, в ip – это p. Значение индексируемого признака изменяется: отчетное значение сопоставляется с базисным.
Признак-вес выполняет функцию веса по отношению к индексируемому признаку; его значение в данном индексе принимается неизменным, так как он не должен искажать оценку изменения индексируемого признака. В Iq признаком-весом является р, а в Ip - q.
Индексируемый признак можно назватьфактором изменения общего результата, а признак-вес -характеристикой условий, в которых оценивается это изменение.
Если индексы рассматриваются в системе, то должна обеспечиваться взаимосвязь между ними. Например, в соответствии с (10.9) должно выполняться равенство
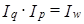(10.11)
Обратимся к формулам (10.11). Каждый из индексов показывает, как изменился тот или иной фактор при неизменности прочих условий: и в формуле индекса Iq и в формуле Ip веса закреплены на базисном уровне. Это обеспечивает сопоставимость оценок изменений факторов. Однако равенство (10.11) не обеспечивается или, как говорят иначе, не обеспечивается увязка индексов в систему:
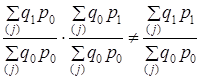
То же происходит, если все индексы будут построены с отчетными весами:
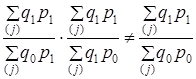
Только когда взаимосвязанные индексы строятся с весами разных периодов, увязка их в систему выполняется:
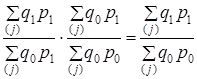(10.12)
или
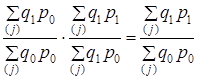(10.13)
Из этих двух вариантов отечественная статистика долгое время отдавала предпочтение второму. Соответственно существовало правило определения периода весов: индексы первичных признаков строятся на весах базисного периода, вторичных - на весах отчетного периода. Это правило признавало неравное значение признаков в системе: первичный признак выступает как основа формирования нового (отчетного) значения результативного признака w1. Этим объясняется то, что индекс первичного признака (например, Ip) оценивает изменение этого признака при сохранении базисных условий, тогда как изменение вторичного признака оценивается уже в изменившихся условиях, когда первичный признак принял значение отчетного периода.
Рассмотрим на примере, как влияет использование разных значений признака-веса на величину индекса (табл. 10.5).
Таблица 10.5
Дата добавления: 2015-01-21; просмотров: 2269;