Данные о продаже продуктов на городском рынке за месяц
| Цена тыс. руб./кг | Продано, т | Выручка, млн ру6. | |||||||
| май | июнь | май | июнь | май | июнь | условная | условная | ||
| p0 | p1 | q0 | q1 | w0 = q0 p0 | w1 = q1p1 | q1p0 | q0 p1 | ||
| Говядина | 15,05 | 15,95 | 3,0 | 2,98 | 45,15 | 47,53 | 44,85 | 47,85 | |
| Свинина | 16,30 | 17,54 | 2,8 | 2,75 | 45,64 | 48,24 | 44,82 | 49,11 | |
| Масло животное | 13,75 | 14,19 | 1,5 | 1,45 | 20,62 | 20,58 | 19,94 | 21,28 | |
| Масло растительное | 5,56 | 5,77 | 1,0 | 0,90 | 5,56 | 5,19 | 5,00 | 5,77 | |
| Картофель | 1,02 | 1,13 | 10,2 | 10,80 | 10,40 | 12,20 | 11,02 | 11,53 | |
| Капуста | 4,12 | 4,08 | 8,5 | 8,8 | 35,02 | 35,90 | 36,26 | 34,68 | |
| Яблоки | 9,24 | 9,26 | 5,7 | 4,9 | 52,67 | 45,37 | 45,28 | 52,78 | |
| Итого | - | - | - | - | 215,06 | 215,01 | 207,17 | 223,00 | |

В обоих вариантах получены показатели снижения объема продажи и роста цен, но в первом случае объем продажи снизился на 3,58%, цены повысились на 3,7%, а во втором - снижение объема продажи на 3,7% и рост цен на 3,78%. Следуя статистической логике, можно сказать, что точечные оценки в принципе невозможны; можно говорить лишь о поле или интервале оценок: для объема продажи - снижение от -3,58% до - 3,7%; для цен - рост от 3,7% до 3,78%.
Однако в практическом использовании индексов стремятся получить однозначное решение тем или иным способом. Первый путь - получение средних оценок изменений: либо в форме индексов, построенных на средних весах:
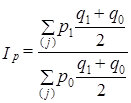
либо через осреднение разновзвешенных индексов. При этом предпочтение отдается средней геометрической:
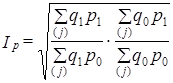 (10.14)
(10.14)
Второй путь основан на предпочтении какого-то одного варианта построения взаимосвязанных индексов. Как уже отмечалось, в отечественной статистике был принят второй вариант. Но при этом возникала несопоставимость оценок изменений признаков. Поэтому делалась попытка построения всех взаимосвязанных индексов на весах одного периода - базисного:
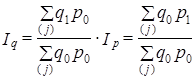 (10.15)
(10.15)
Понятно, что в этом случае не выполняется увязка индексов в систему:
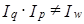
Изолированная оценка изменения каждого фактора при неизменности другого приводит к недоучету эффекта совместного изменения факторов. Скажем, вы смотрите движущееся изображение без звука или слушаете звуковое сопровождение без изображения, и в том, и в другом случае воздействие меньше, чем при соединении изображения и звука. Наглядно это можно показать с помощью особого вида плоскостной диаграммы, известной в отечественной статистике как «знак Варзара» (по имени русского статистика В. Е. Варзара (1851-1940) (см. рис. 10.1).
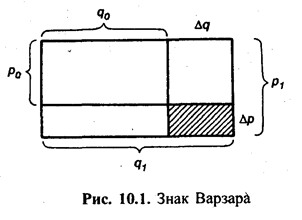
Результативное явление представлено здесь в виде прямоугольника, площадь которого в базисном периоде 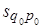 , в отчетном -
, в отчетном - 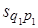 . Переход от базисного состояния к отчетному формируется за счет изменения фактора
. Переход от базисного состояния к отчетному формируется за счет изменения фактора 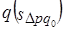 , изменения фактора
, изменения фактора 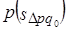 и совместного изменения обоих факторов
и совместного изменения обоих факторов 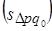 :
:
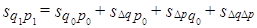 (10/16)
(10/16)
В статистической науке выработано множество версий такого разложения: 1) выделение эффекта взаимодействия факторов в самостоятельный член; 2) присоединение его к какому-либо одному фактору (т. е. построение какого-либо из индексов на весах отчетного периода); 3) разделение эффекта взаимодействия факторов и присоединение к изменениям факторов - поровну, либо пропорционально значениям индексов факторов, либо еще по какому-то принципу. Вы можете тоже попытаться предложить свое решение - актуальность проблемы сохраняется.
В. И. Борткевич (1868-1931) вывел формулу, объясняющую различие между индексами с разными весами:
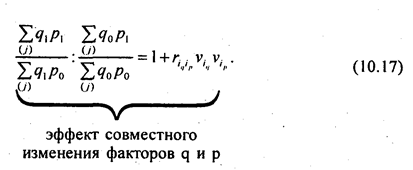
Точно так же можно выразить соотношение между индексами фактора q с разными весами. Из формулы (10.17) ясно, что индексы с отчетными и базисными весами будут равны, если выполняется хотя бы одно из условий: или корреляция между изменениями цен и объема продажи на отдельные товары отсутствует, 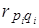 = 0; или темпы изменения объемов товаров всех видов будут oдинаковы,
= 0; или темпы изменения объемов товаров всех видов будут oдинаковы, 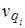 = 0; или темпы изменений цен на все товары будут одинаковы,
= 0; или темпы изменений цен на все товары будут одинаковы, 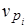 = 0. Чем большая дистанция разделяет сравнимые периоды, тем сильнее проявляются все отмеченные факторы различий между индексами с разными весами.
= 0. Чем большая дистанция разделяет сравнимые периоды, тем сильнее проявляются все отмеченные факторы различий между индексами с разными весами.
Ничего не меняется, если результативный признак включает более двух факторов, т. е. в случае мультипликативной модели:
y = x1 ·x2…..xk
Если придерживаться концепции неравноправия факторов и строить индексы с разными весами, то все зависит от принятой последовательности факторов в системе. Например, общие затраты на кожу для изготовления женских туфель можно представить как w = qlp, где q - количество пар туфель; l - средний расход кожи на одну пару; р - цена кожи. Первым стоит фактор q как первичный, с которого и начинаются все изменения. Тогда индексы будут иметь вид:
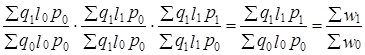 (10.18)
(10.18)
Здесь используется то же правило выбора весов, которое было сформулировано выше. Признаки, стоящие слева от индексируемого признака, трактуются по отношению к нему как первичные и закрепляются на отчетном уровне (они «уже» изменились), стоящие справа от него трактуются как вторичные и закрепляются на базисном уровне (они как бы «еще» не изменились). К этому добавляется условие содержательной интерпретации при последовательном объединении признаков слева направо. Скажем, произведение ql имеет экономический смысл — это расход кожи на весь объем производства туфель, при перестановке признаков q, р, l произведение qp экономического смысла не имеет. На таком подходе основан метод цепных подстановок, широко используемый в экономическом анализе. \
Если же все индексы строятся на весах одного и того же (базисного) периода, то последовательность признаков не имеет значения. Система индексов будет иметь вид:
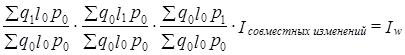 (10/19)
(10/19)
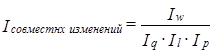
И в этом случае многофакторной модели эффект совместных изменений можно либо сохранить как самостоятельный член разложения, либо распределить между изменениями факторов. Это зависит от поставленной задачи и от пристрастий исследователя.
Сравнение данных отчетного и базисного периодов неявно предполагает представление экономических процессов в виде дискретной последовательности периодов времени, что особенно проблематично при сравнении в длительном периоде. Экономические индексы для моментов непрерывного времени были предложены в 1928 г. французским статистиком Ф. Девизиа. Это привело к использованию в индексном анализе дифференциального исчисления. Данный подход до сих пор не вошёл в статистическую практику, однако теоретически он более обоснован, нежели традиционные методы.
Дата добавления: 2015-01-21; просмотров: 1377;
