Индекс структуры

Индексы позволяют анализировать изменения не только агрегатов, но и средних величин. Предположим, изучается динамика средней цены товара на трех рынках города, расположенных в разных районах - центральном и двух периферийных - старой и новой застройки. Уровень цен в этих районах разный, соответственно на среднюю цену продажи на колхозных рынках влияют не только цены на каждом из них, но и доля каждого рынка в общем объеме продажи.

Формула средней цены:

где р_i - цена товара на i-м рынке.

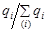- структура продажи.

Изменение средней цены (как и любой взвешенной средней) выражается индексом:

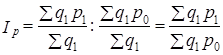
Этот индекс получил название индекса переменного состава, так как отражает не только изменение осредняемого признака р, но и структуры совокупности 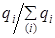. На основе индекса средней величины могут быть построены индекс самого осредняемого признака при постоянстве структуры совокупности и индекс структуры:

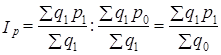(10.23)

Этот индекс получил названиеиндекса постоянного состава.

Соответственно

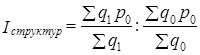(10.24)

Формулы индексов (10.23) и (10.24) основаны на общепринятом правиле, по которому структура совокупности как первичная характеристика при индексации цен закрепляется на уровне отчетного периода, а цены как вторичная характеристика при индексации структуры закрепляются на уровне базисного периода. Очевидно, что применение весов разных периодов и в этом случае обеспечивает выполнение равенства:

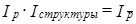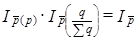или (10.25)

Конечно, можно все индексы построить на весах базисного периода, и это будет правильнее с точки зрения оценки изменения каждого из факторов, но тогда равенство (10.25) будет нарушено.

Рассмотрим построение этих индексов на примере. На трех рынках города продается картофель. Данные о продаже за день в зарегистрированных ценах приведены в табл. 10.6.

Таблица 10.6