Границы и условия применения индексного

Метода

Каждый метод ориентирован на особые представления изучаемого объекта, на особую его модель. Индексный метод предполагает, что связь между признаками являетсяжестко детерминированной, которая проявляется как в каждом отдельном случае (для отдельного товара, вида продукции, предприятия и т. д.), так и в совокупности. Связь, изучаемая с помощью индексов, выражается в видеуравнения связи:

либо мультипликативного

у = х₁x₂...х_k

либо аддитивного

у = х₁ + х₂ + ... + х_k,

Вид функции, число переменных факторов (сомножителей или слагаемых) определяются нашими представлениями о логике изучаемой связи. Многофакторная мультипликативная модель строится путем последовательного расчленения одного из факторов на составляющие.

Например, можно записать следующее уравнение связи:

Эту модель можно детализировать. Она будет включать не два, а пять факторов:

Если мультипликативная модель имеет в качестве результативного первичный признак, то она называется полной[15] .Примером такой модели является вышеуказанная модель. Разделив обе части равенства на первый фактор, получим неполную модель среднечасовой выработки работника.

Представление связи как жестко детерминированной является условным, так как связи социально-экономических явлений носят стохастический характер.

Если представить мультипликативную модель как двухфакторную, т.е. у = x₁x₂, то в целом по совокупности уравнение имеет вид у = ах. Коэффициент а является коэффициентом связи между у и х. Он передает прямое влияние фактора х на результат у. Для нашего примера величина отработанных человеко-часов передает влияние среднечасовой выработки на объем продукции. Однако выработка влияет на результат не только непосредственно, но и через другие факторы: уровень выработки может определять численность рабочих, их долю в списочном составе, фактическую продолжительность рабочего дня. В корреляционном анализе, измеряя корреляцию между результатом и фактором, мы получаем полную меру корреляции независимо от того, как реализуется связь — непосредственно или опосредованно. В индексном анализе мы измеряем только прямое влияние изменения фактора на изменение результата.

При построении уравнения связи иногда допускаются отступления от логики ради обеспечения увязки признаков, получения жестко детерминированного выражения связи. Поэтому можно встретить уравнения связи, в которых не все составляющие элементы экономически обоснованы, нередки случаи появления среди факторов обратных величин.

Приведем пример недостаточно обоснованного уравнения связи:[16]

Трудно представить, чтобы рост доли основных фондов вызывал рост балансовой прибыли.

При мультипликативной связи индексов относительные выражения приростов факторов связаны аддитивно. Например,

Чем больше различаются индексы отдельных факторов, тем больше сумма относительных приростов отличается от темпа прироста результата. Например,

Если известно, что значение первого индекса 1,2, второго - 1,05, то

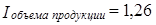, тогда как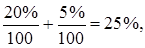

т. е. переход от темпов роста к темпам прироста приводит к определенным трудностям в интерпретации количественного влияния факторов на результат.

Наконец, решение вопроса об измерении эффекта отдельных факторови их совместного изменения всегда условно.

Все предыдущее изложение было ориентировано на мультипликативную модель. При аддитивной связи признаков индексный анализ проводится по следующей формуле:

,

т. е. общее изменение результата зависит от изменения каждого фактора и его доли в базисной величине результата. Приведем пример (табл. 10.8).

Таблица 10.8