И регрессионного методов анализа
Применяя индексный анализ часто ощущается недостаточность использования только этого метода прежде всего из-за того, что уравнение связи как жестко детерминированная функция может быть построено лишь для «ближайшего» круга факторов, тех, которые непосредственно составляют результат. Такие факторы могут оказаться недостаточными для объяснения его динамики. Эта особенность анализа связи на основе жестко детерминированного выражения результата очевидна, например, при постатейном анализе себестоимости продукции. Вроде бы такой анализ обеспечивает точность показателей связи. Так, если изменится норма расхода того или иного материала и заготовительные расходы на него, можно точно указать, на какую величину снизится (повысится) себестоимость продукции данного вида. Вместе с тем «функциональный» анализ себестоимости продукции вскрывает лишь непосредственное различие себестоимости из-за различий величин, прямо входящих в ее расчет, но не вскрывает причин самих этих различий. Можно установить, насколько на предприятиях, производящих однородную продукцию, различаются нормы расхода сырья, сдельные расценки и т.п. Но само по себе выяснение этих факторов еще ничего не говорит об их причинах, которые зависят от уровня технического оснащения предприятия, квалификации его работников, организации производства и т.п. Эти факторы воздействуют на величину себестоимости не непосредственно, а через величины, прямо учитываемые в ее расчетах: через нормы расхода материалов, расценки и ставки заработной платы, суммы амортизации и другие виды производственных затрат. В отличие от ближайших факторов такие факторы принадлежат к другому, так сказать, «глубинному уровню изучаемой структуры.
Далеко не всегда можно выявить механизмы связи между глубинными причинами и результатом в силу их большей отдаленности, многоплановости влияния. Не всегда можно включить их в жестко детерминированное уравнение связи путем последовательного развертывания признаков. Это приводит к комплексному использованию методов, основанных на жесткой детерминации признаков, и методов, не ориентированных на такой характер связей.
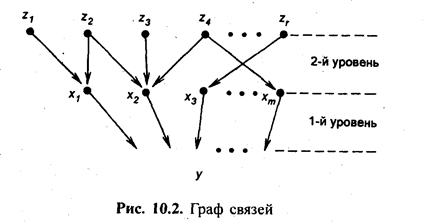
Понять в полной мере задачи интеграции разных методов статистического изучения связей можно с помощью графа связей.Граф связей учитывает непосредственные, т. е. причинные связи, которые предполагают изменение х, при изменении влияющего на него х при постоянстве всех прочих факторов. Асимметричность причинных связей отражается в направленности дуг графа (дуга - соединение вершин графа, т.е. точек, соответствующих элементам структуры).
Нередко оказывается, что разобраться в системе связей можно только тогда, когда граф связей будет включать не только факторы - признаки данной единицы совокупности, непосредственно определяемые в процессе ее функционирования(эндогенные), но и факторы, не зависящие от нее, но влияющие на изучаемый результат(экзогенные). Если первые образуют систему признаков и могут находиться в жестко детерминированной связи с изучаемой результативной переменной вследствие устойчивости связи в рамках единицы совокупности, то вторые не являются признаками изучаемой единицы, потому их связь с результатом неустойчива, стохастична. Как правило, действие экзогенных факторов опосредовано эндогенными переменными, формирующими результат. Потребность сочетания разных уровней анализа - «вышележащего», на котором могут иметь место жестко детерминированные связи, и «нижележащего», на котором они отсутствуют, вызываетинтеграцию разных методов анализа. Например, изучая, почему произведен тот или иной объем валовой продукции, весьма важно не останавливаться на анализе уравнения связи, подобного приведенному в п. 10.7, включающего признаки, определяемые на уровне предприятия, а перейти на другой уровень анализа. Выявить, например, чем обусловлена та или иная величина среднечасовой выработки рабочих. Для этого необходимо перейти к совокупности рабочих и их признакам (уровню квалификации, стажу, умению организовывать npoueqc труда и т. д.).
На рис. 10.2 изображен гипотетический граф связей, в котором элементы «высшего» уровня структуры обозначены как хj(j = 1,2,..., т). Это факторы, находящиеся в жесткой связи с результатом (у);. z1 - глубинные факторы, принадлежащие другому уровню изучаемой структуры связей (l = 1,2,...,г). Эти факторы находятся в стохастической связи с хj и у.
Рис. 10.2 показывает, что используя индексы (или другой метод анализа, основанный на жестко детерминированных связях) мы ограничиваемся только одним уровнем структуры связей, включающим отношения между у и хj и не затрагиваем связи между z1 и хj. Используя только этот путь анализа, мы можем не выяснить причины изменения результата. Кроме того, в анализе только жестко детерминированных связей [xj ® y], каждый из хj выступает как независимая величина, тогда как они могут быть связаны, как непосредственно, так и через общие детерминирующие факторы. Эта связь является стохастической и может быть измерена с помощью соответствующих методов.
Методика комплексного использования индексного и регрессионного анализа такова. Определяется жестко детерминированное уравнение связей у =f(x1,..., хm), на основе графа связей строится уравнение регрессии для каждой компоненты (хj):
x̂j = a0 +a1z1 +….+ a2z2,
где z1 - так называемые глубинные причины.
Оценив значимость параметров отдельных регрессий, устанавливается круг причин для каждого из хj, общий круг причин для хj и хi (i ≠ j). Используя полученное на основе регрессии значение хj, мы получаем возможность измерить влияние каждого из учтенных в регрессии факторов на у. Таким образом в анализе участвуют функционально и нефункционально связанные факторы.
Остановимся подробнее на методике комплексного использования методов. Рассмотрим простейший случай. Пусть изучаемый результативный признак может быть представлен как жестко детерминированная двухфакторная мультипликативная функция у = xw (несмотря на то, что оба фактора х и w принадлежат одному и тому же уровню изучаемой структуры, мы обозначили их по-разному для того, чтобы облегчить изложение методических вопросов). Пусть х -первичный (объемный) признак, w - вторичный (так называемый количественный) признак. Тогда система аналитических индексов имеет вид:
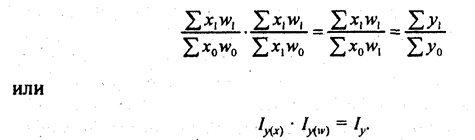
На следующем этапе анализа перейдем на другой уровень структуры связей. Введем различные обозначения для факторов, влияющих на x и на w:
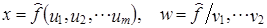
Заметим, что в принципе, как уже отмечалось, круг факторов для и w может частично совпадать. В случае непосредственной связи между х и w, та из переменных, которая является независимой, может включаться в регрессию другой (зависимой) переменной. Положим, что круг объясняющих переменных для х и w остался неизменным в отчетном периоде по сравнению с базисным. Принимая регрессии линейными, имеем по две регрессии для х и w, описывающих базисное и отчетное состояние х и w.
Для базисного периода:
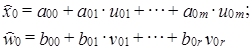
Для отчетного периода:
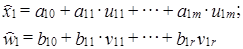
где первый подстрочный значок в каждой регрессии обозначает период, к которому она относится, второй - номер параметра или переменной, соответственно.
Введем в индекс Iy(x) расчетное значение x̂, получим следующую систему индексов:
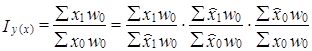 (10.38)
(10.38)
Первый и последний индексы этой системы (10.38) измеряют влияние факторов, не учтенных в регрессии 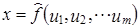 . Сравнение этих индексов позволяет установить, регрессия какого периода точнее описывает фактические данные. Если регрессии построены правильно, то расхождения фактических и расчетных значений х и для базисного и для отчетного периодов будут незначительны, и оба индекса будут близки к единице.
. Сравнение этих индексов позволяет установить, регрессия какого периода точнее описывает фактические данные. Если регрессии построены правильно, то расхождения фактических и расчетных значений х и для базисного и для отчетного периодов будут незначительны, и оба индекса будут близки к единице.
Центральная роль принадлежит второму индексу системы - он измеряет влияние на у изменений в расчетных значениях х̂. Расхождение между 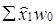 и
и 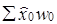 может возникнуть как вследствие изменений значений переменных u1, ..., иm, так и в результате изменений силы их влияния на х- коэффициентов регрессий а11, а12 ...,a1m по сравнению с a01, а02, ..., а0m. Раздельную оценку влияния на у глубинных факторов и и силы их воздействия а можно получить на основе специальной системы индексов. При этом рекомендуется первичным считать значение переменной, а вторичным - коэффициент регрессии[17].
может возникнуть как вследствие изменений значений переменных u1, ..., иm, так и в результате изменений силы их влияния на х- коэффициентов регрессий а11, а12 ...,a1m по сравнению с a01, а02, ..., а0m. Раздельную оценку влияния на у глубинных факторов и и силы их воздействия а можно получить на основе специальной системы индексов. При этом рекомендуется первичным считать значение переменной, а вторичным - коэффициент регрессии[17].
Получим:
а) систему индексов, измеряющих влияние на у изменения значений переменных и:
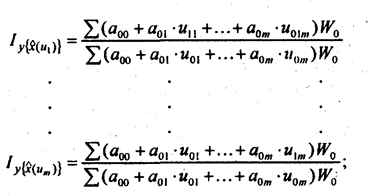
б) систему индексов, измеряющих влияние на у изменений интенсивности связей между х и и(а1):
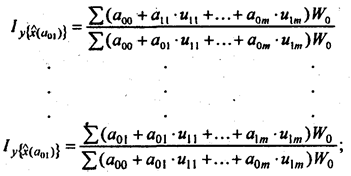
в) индекс, учитывающий изменение свободного члена уравнения регрессии (а0):
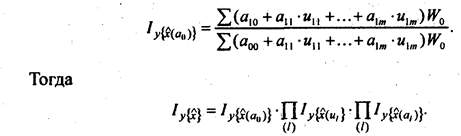
Очевидно, что на основе приведенных формул могут быть получены и соответствующие абсолютные эффекты
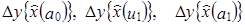
Точно так же может быть проанализировано влияние на факторов, детерминирующих W.
Покажем применение описанной методики анализа на условном примере. Предположим, что изучается работа каменноугольных шахт одного треста. В качестве результативного признака выступает среднесменный объем добычи угля (W), который может быть представлен как произведение двух факторов: численности рабочих на подземных работах (N) и среднесменной добычи угля на одного подземного рабочего (F) - W = N- V. По данным табл. 10.10 определим, как изменился среднесменный объем добычи угля в целом по тресту в отчетном периоде по сравнению с базисным и как на это изменение повлияло изменение численности подземных рабочих и среднесменной добычи на одного рабочего.
Таблица 10.10
| № шахты | Базисный период | Отчетный nepиод | Условный среднесменный объем добычи, т | |||||
| средне-сменная добыча на 1 подземного рабочего, т | число подземных рабочих | среднесменный объем добычи, т | средне-сменная добыча на 1 подземного рабочего, т | число подземных рабочих | среднесменный объем добычи, т | |||
| A | V0 | N0 | W0 | V1 | N1 | W1 | N1V0 | |
| å | X | X | ||||||
Среднесменный объем добычи угля в целом по тресту увеличился:
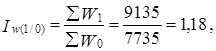
объем добычи вырос на 18%, что составило в абсолютном выражении 1400 т.
Численность подземных рабочих в данный период увеличилась и за счет этого среднесменный объем добычи вырос следующим образом:
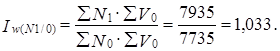
Как видим, этот фактор в меньшей степени способствовал росту общего объема добычи. За счет него объем добычи вырос только на 3,3% или на 260 т.
Основная роль в общем изменении результата принадлежит интенсивному фактору - росту среднесменной добычи угля на одного подземного рабочего:
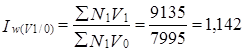
т. е. за счет роста среднесменной добычи угля на одного подземного рабочего общий объем добычи вырос на 14,2% или на 1140 т. Вычисленные индексы образуют систему индексов:
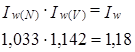
Как отмечает Г. И. Бакланов, влияние каждого фактора на относительное изменение общей абсолютной величины можно получить, выразив соответствующую абсолютную разность в процентах к общей абсолютной величине в базисном периоде[18]. Вычисляя относительное влияние факторов таким образом, мы получим аддитивное разложение относительного изменения результативного признака. При этом относительная оценка влияния первичного признака (N) будет той же самой (+3,3%), а относительная оценка влияния вторичного признака (v) изменится и составит:
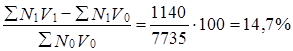
Тогда 3,3% + 14,7% = 18,0%
Ввиду того, что основная роль в общей динамике объема добычи принадлежит производительности труда - среднесменной добыче одного подземного рабочего, на следующем этапе анализа рассмотрим, за счет каких факторов сложится тот или иной уровень производительности труда и как изменение этих факторов сказалось на величине общего объема среднесменной добычи угля по тресту.
Среднесменная добыча подземного рабочего определяется многими факторами, среди которых можно назвать как характеристики рабочих (стаж, квалификация и т. д.), так и характеристики условий труда (используемая техника, степень механизации производственных процессов и др.) и разрабатываемого угольного пласта (длина лавы, мощность пласта и т. д.). Все эти факторы имеют стохастическую связь со среднесменной добычей рабочего, через нее оказывая влияние на общий объем добычи. Предположим, что из всего множества факторов главными и в отчетном и в базисном периодах оказались только два: мощность пласта и уровень механизации навалки угля. Данные по этим факторам по каждой из десяти шахт приведены в табл. 10.11.
Таблица 10.11
| № шахты | Базисный период | Отчетный период | |||||
| средне-сменная добыча на 1 подземного рабочего, т | мощность пласта, м. | уровень механизации навалки угля, % | средне-сменная добыча на 1 подземного рабочего, т | мощность пласта, м | уровень механизации навалки угля, % | ||
| А | V0 | М0 | К0 | V1 | М1 | К1 | |
Прежде всего определим средние значения признаков, средние квадратические отклонения и коэффициенты вариации (табл. 10.12).
Таблица 10.12
| Период | Средние величины | Средние квадратичекие отклонения | Коэффициенты вариации | ||||||
| V | М̅ | К̅ | SМ. | SM | Sk | VV | VM | Vk | |
| Базисный Отчетный | 7,5 8,5 | 99,0 96,4 | 69,0 74,0 | 2,01 2,73 / | 15,80 17,46 | 19,81 19,73 | 26,8 32,1 | 16,0 18,1 | 28,7 26,7 |
Сравнение отчетных данных с базисными свидетельствует: о возрастании средних значений тех признаков, которые отражают функционирование шахт (эндогенных); среднее значение экзогенного признака - мощности пласта - несколько снизилось. Возросла вариация шахт по величине среднесменной выработки одного подземного рабочего и по мощности пласта, тогда как по уровню механизации навалки угля наметилось некоторое выравнивание данных.
Вычисленные значения коэффициентов парной корреляции указывают на тесную связь между признаками (табл. 10.13).
Таблица 10.13
| Период | rvм | rvм | rмk |
| Базисный Отчетный | 0,903 0,893 | 0,726 0,761 | 0,819 0,780 |
И в том и в другом периоде среднесменная добыча рабочего теснее коррелирует с мощностью пласта, нежели с уровнем механизации навалки угля. Однако наметилось некоторое снижение величины rvm при повышении rvм Сравнение коэффициентов парной корреляции зависимой переменной {V) с независимыми переменными и корреляции последних между собой свидетельствует о ко-линеарности факторов - их тесной линейной связи. При таком соотношении нецелесообразно построение множественной регрессии, куда бы входили оба названных фактора - и мощность пласта и коэффициент механизированной навалки угля. Поэтому построим парную регрессию, описывающую зависимость среднесменной добычи одного рабочего только от мощности пласта: v̂ = а + b. Для базисного периода уравнение парной регрессии:
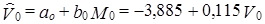 ;
;
для отчетного периода:
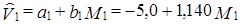
Так как вариация зависимой переменной превосходит вариацию независимой переменной (vv > vM), свободный член уравнения регрессии в обоих периодах - отрицательная величина (а < 0). Сравнение коэффициентов регрессии b0 и b1 показывает, что сила влияния данного фактора на среднесменную добычу рабочего растет, а теснота связи падает ( 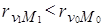 ). Если коэффициент детерминации в базисном периоде составил
). Если коэффициент детерминации в базисном периоде составил 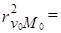 81,54%, то в отчетном
81,54%, то в отчетном 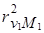 = 79.74%.
= 79.74%.
Мощность пласта не входит в жестко детерминированное выражение общего среднесменного объема добычи угля, которое мы анализировали с помощью индексов. Однако этот фактор так же может быть учтен в анализе через регрессию v = f̅(M) и включение в индексы расчетных значений v̂. В этом случае индекс, характеризующий влияние изменения среднесменной добычи одного подземного рабочего на величину общей среднесменной добычи угля, должен быть представлен как произведение трех индексов:
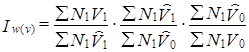
Расчетные значения среднесменной добычи угля на одного подземного рабочего и соответствующие расчетные значения общей среднесменной добычи представлены в табл. 10.14.
Подставляя в записанную систему индексов расчетные значения среднесменного объема добычи, получаем:
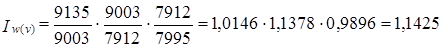
Сопоставление первого и последнего индексов показывает, что базисная регрессия v = f̂(M) точнее описывает исходные данные. Этого следовало ожидать, так как 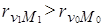 . Средний из трех индексов отражает динамику среднесменного объема добычи под влиянием мощности пласта. В соответствии с изложенной выше методикой этот индекс можно разложить на частные индексы, отражающие влияние изменения величины мощности пласта:
. Средний из трех индексов отражает динамику среднесменного объема добычи под влиянием мощности пласта. В соответствии с изложенной выше методикой этот индекс можно разложить на частные индексы, отражающие влияние изменения величины мощности пласта:
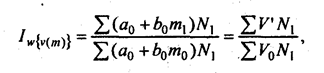
Таблица 10.14
| № шахты А | Расчетные значения | |||||||
| Среднесменной добычи одного рабочего, т* | Среднесменного объема добычи | |||||||
| 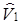
| 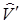
| 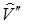
| 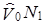
| 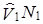
| 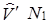
| 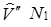
| |
| 3' | 4,9 8,5 9,4 7,4 6,6 10,5 5,9 9,2 4,9 7,7 | 5.4 10,1 11,0 8,3 7,3 12,5 6,9 11,1 4,8 7,6 | 4,6 8,5 9,2 7,0 6,2 1.0,5 5,9 9,3 4,2 6,5 | 6,5 11,2 12,1 9.4 8,4 13.6 8,0 12,2 5,9 8,7 | ||||
| Итого | х | X | X | X | ||||
| * V̂0 = a0 +b0M0 V̂1 = a1 +b1M1 V̂¢ = a0 +b0M1 V̂² = a0 +b1M1 |
Изменение силы воздействия этого признака на выработку и, соответственно, на общий объем добычи:
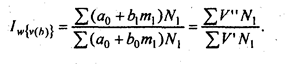
Для увязки этих частных индексов следует ввести корректирующий индекс, отражающий изменение свободного члена уравнения регрессии v по М:
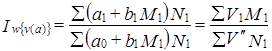
Все величины, требуемые для расчетов этих индексов, представлены в табл. 10.14. С учетом этого
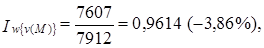
т. е. за счет наблюдаемого в отчетном периоде снижения мощности пласта среднесменная добыча угля сократилась в целом по тресту на 3,86% или на 305 т. Сокращение мощности пласта происходило, как уже было выявлено, наряду с усилением влияния этого фактора - коэффициент регрессии в отчетном периоде выше, чем в базисном (b1 = 0,140, b0 = 0,115). Повышение силы влияния мощности пласта на среднесменную выработку, а через нее на объем добычи характеризует следующий индекс:
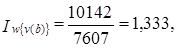
т. е. за счет роста силы связи общий объем среднесменной добычи вырос на 33,3% или на 2535 т. Влияние изменения свободного члена уравнения регрессии - параметра а - оценивается следующим индексом:
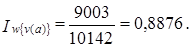
Этот результат никак не комментируется, как и сам параметр а, он не может быть содержательно интерпретирован.
Рассмотренный пример показывает, что подобный анализ основан на определенной условности. Так, оценку влияния изменения коэффициента регрессии мы проводим при базисном значении свободного члена уравнения, тогда как параметры уравнения регрессии связаны друг с другом. Все они получаются в результате решения одной и той же системы уравнений. То же можно сказать в отношении раздельной оценки изменения значения фактора и силы его влияния. Тем не менее, соединение индексного и регрессионного методов обогащает анализ, позволяет ввести в него нефункционально связанные факторы.
Рассмотренная методика анализа позволяет измерить влияние факторов, непосредственно не входящих в жестко детерминированное выражение результативного признака, не только в целом по совокупности, но и по каждому единичному явлению.
Проведение анализа по отдельным единицам с использованием уравнения регрессии обычно основывается на разложении величины отклонения от общей средней (уi - у̅) на две составляющие (у̂i - у̅) и (уi - у̂i). Если в уравнение регрессии входят все важные и существенные факторы, от которых зависит величина результативного признака, и коэффициент детерминации близок к единице, то остальные, не включенные в уравнение факторы, характеризуют индивидуальные, несущественные особенности, зачастую не имеющие количественного выражения. В этом случае разница (уi - у̂i) образуется за счет несовпадения интенсивности воздействия на у всех учтенных факторов в условиях данной i-й единицы и средней интенсивности их воздействия, выраженной в величинах коэффициентов регрессии, входящих в расчетное значение ŷi. Это дает право интерпретировать разницу (уi - у̂i) или отношение уi / у̂i как показатель того, как эффективность использования учтенных факторов у i-й единицы соотносится со средней эффективностью их использования. Разница (у̂i -у̅) возникает за счет различия в значениях учтенных факторов для данной i-и единицы и в среднем по совокупности. Такое разложение дает возможность выявить резервы, имеющиеся у каждой отдельной единицы, в части эффективности использования факторов и в части их уровня.
При анализе взаимосвязей в сочетании с изучением динамики явлений нас интересует в первую очередь не соотношение индивидуального и среднего по совокупности значений результативного признака, а изменение его состояния в отчетном периоде по сравнению с базисным - (у1 – y0). В случае использования регрессионного анализа эта разница может быть представлена следующим образом:
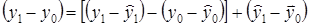
Первый член разложения характеризует изменение в величине y вызванное как изменением влияния тех неучтенных в регрессии факторов, которые не коррелируют с учтенными, так и изменением соотношения индивидуальной и средней силы влияния на у учтенных в регрессии факторов. Второй член этого разложения характеризует изменение в величине y, вызванное изменением в значениях факторов, учтенных в регрессии, и изменением средней силы их воздействия на у.
Продолжая наш пример, проведем анализ изменения среднесменной добычи угля, приходящейся на одного подземного рабочего (v), по данным отдельных шахт. Все необходимые величины приведены в табл. 10.15.
Таблица 10.15
| № шахты | ΔV | V0 - V̂0 | V1 - V̂1 | Δ(V0 - V̂) | V̂1 - V̂0 | ΔV̂(м) | ΔV̂(a,b) |
| -1 | 0,1 1,5 -0,4 -0,4 -0,5 -1,5 0,1 1,8 0,1 -0,7 | -0,4 1,9 1,0 0,7 -0,3 -2,5 0,1 0,9 0,2 -1,6 | -0,5 0,4 1,4 1,1 0,9 -1,0 -0,9 0,1 -0,9 | 0,5 1,6 1,6 0,9 0,7 2,0 1.0 1,9 -0,1 -0,1 | -0,3 -0,2 -0,4 -0,4 0,1 -0,7 -1,2 | 0,8 1,6 1,8 1,5 1,1 2,0 1,0 1,8 0,6 1,1 |
Учитывая сравнительно низкие значения отчетного и базисного коэффициентов детерминации (r20 = 0,8154, r21 = 0,7974), разница фактической и расчетной величин (Vi - V̂i) выражает не только различия в эффективности использования учтенного фактора - мощности пласта - на данной конкретной шахте по сравнению со средней эффективностью по тресту, но и влияние неучтенных в уравнении регрессии факторов.
В среднем среднесменная добыча одного подземного рабочего увеличилась в отчетном периоде по сравнению с базисным на 1 т. Мощность пласта снизилась в среднем на 2,6 м. Если бы действовал только этот фактор, то средняя добыча снизилась бы на 0,3 т. Таким образом, весь прирост среднесменной добычи вызван действием прочих факторов.
Увеличение абсолютной величины - свободного члена уравнения регрессии параметра а - является следствием снижения тесноты прямолинейной связи между мощностью пласта и среднесменной добычей угля на одного подземного рабочего. Данные табл. 10.15 позволяют определить значимость изменения мощности пласта и прочих факторов в общем изменении величины среднемесячной добычи, приходящейся на одного подземного рабочего на мжди шахте. Так, нулевое приращение среднесменной выработки на р вой шахте явилось результатом равнодействия отрицательною яния снижения мощности пласта и других факторов и общей тенденции повышения «съема» угля с одного метра мощности. На второй шахте прирост среднесменной добычи одного рабочего обусловлен, с одной стороны, более эффективным использованием мощности пласта, нежели в среднем по тресту, с другой - положительным влиянием изменения прочих факторов, как коррелирующих с мощностью пласта, так и не связанных с ним. Подобные заключения можно сделать по третьей, четвертой и т. д.
Таким образом, введение в жестко детерминированное уравнение связи величин, найденных на основе уравнения регрессии, позволяет учесть в комплексе как жестко детерминированные, так и стохастические связи.
В экономическом анализе часто решаются задачи, связанные сизучением средних величин, их уровня и динамики - какова средняя цена 1 кг ржаного хлеба, говядины, средняя заработавя плата в промышленности, в экономике в целом и т. д. Изменение средней величины отражает индекс
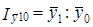
По данным отчетного и базисного периодов можно построить регрессии - обязательно с одним и тем же набором объясняющих переменных:
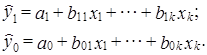
Поскольку, как известно из гл. 8, у̅ = а + b1x̅1 +…+ bkx̅k, отчетная и базисная регрессии могут быть использованы для анализа изменения среднего уровня, у̅.
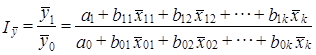 (10.39)
(10.39)
Средняя величина, y̅, может изменяться, во-первых, за счет изменений средних значений объясняющих переменных х̅j в отчетном периоде по сравнению с базисным, во-вторых, за счет изменения коэффициентов регрессии bj, в-третьих, за счет изменения значения свободного члена уравнения регрессии а0.
Соответственно получаем систему индексов:
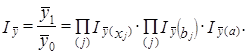 (10.40)
(10.40)
Чтобы обеспечить это равенство, нужно принять какое-то правило индексации. Например, в соответствии с уже высказанным положением сначала индексируются все x̅j при постоянных (базисных) значениях коэффициентов регрессии и свободного члена, затем индексируются коэффициенты регрессии при постоянных (отчетных) средних значениях x̅j, затем индексируется свободный член урвнения регрессии при постоянных (отчетных) значениях как x̅j , так и bj.
Применим рассмотренную методику к анализу среднесменной добычи угля одним рабочим. Среднесменная добыча одного подземного рабочего: базисная – 7,6 т/чел; отчетная – 8,5 т/чел. (табл. 10.12). Были построены базисная и отчетная регрессии, описывающие связь между среднесменной добычей (у) и мощностью пласта (х).
Подставляя средние значения х̅ и у̅. получим.
- 3.885 + 0,115·99,0 = 7,5 (т/чел.);
- 5,0 + 0,140·96,4 = 8,5 (т/чел.).
Измерим, как изменилась среднесменная добыча рабочего и как на нее повлияло изменение средней мощности пласта (х̅), силы влияния этого фактора на добычу (b) и корректирующего параметра, т.е. свободного члена уравнения регрессии (а):
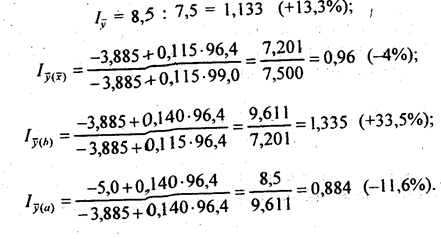
Таким образом, рост среднесменной добычи угля был обусловлен усилением использования такого фактора как мощность пласта - ростом его воздействия на добычу на 33,5%. Сама мощность пласта несколько уменьшилась, что привело к снижению средне-сменной добычи на 4%. Изменение свободного члена тоже оказало негативное влияние на среднесменную выработку (-11,6%).
Все полученные индексы образуют систему индексов: их произведение равно индексу среднесменной добычи.
Дата добавления: 2015-01-21; просмотров: 1023;
