Данные розничной торговли города
| № п/п | Относительное изменение количества купленных продуктов в июне по сравнению с маем, % ip =q1 : q0 | Выручка в июне, млн руб. q1·p1 | Условная выручка без учета изменения цен, млн руб., q1·p0 = q1·p1 : ip |
| 98,5 | 2560,0 . | 2316,7 | |
| 100,3 | 827,2 | 737,3 | |
| 97,8 | 2077,1 | 2012,7 | |
| 102,0 | 10,6 | 10,0 | |
| 100,0 | 903,2 | 882,0 | |
| 98.0 | 2780,3 | 2591,1 | |
| Итого | 596,6* | 9158,4 | 8549,8 |
| * Обычно iq не суммируется. |
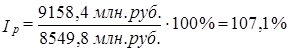
Результат совпал с тем значением / , которое было получено по формуле (10.2). Но это случайное совпадение, которое оказалось возможным из-за слабой корреляции между изменением уровня цен и объема продаж отдельных товаров. Это может быть при сравнении за короткий период. В рыночной экономике взаимосвязь между колебаниями цен и объема продаж проявляется при сравнении за более длительный период. Ниже будет показано, как измерить величину этой корреляции (см. формулу (10.17).
Знаменатель формулы (10.6) имеет смысл затрат на покупку «отчетного» количества товаров по базисным ценам:
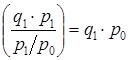
Тогда формула (10.6) может быть представлена как
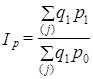(10.7)
Эта формула индекса цен была предложена Пааше в 1874 г. Различие между индексами Пааше и Ласпейреса, их использование обсуждаются ниже в данной главе.
Итак, мы рассмотрели применение разных форм и видов средних величин для определения среднего изменения цен по всем товарам. Люди всегда в первую очередь интересовались ценами и их изменениями. Но такой же подход может быть применен к оценке сводных изменений других характеристик, например объема (количества) покупок товаров. Кстати заметим, что используемые нами обозначения цен (р), количества (q) неслучайны и соответствуют начальным буквам английских слов price (цена) и quantity (количество). Это закрепленные обозначения в статистике.
Таким образом, общее изменение количества проданных товаров формируется как среднее по отношению к изменениям объема покупок отдельных товаров, т. е.
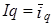, где 
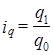
Возникает вопрос о порядке расчета средней из iq: средняя арифметическая - простая или взвешенная - или другая форма средней. Ограничимся рассмотрением только средней арифметической.
По данным табл. 10.4 простая средняя арифметическая из индивидуальных индексов количества равна:
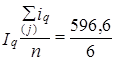= 0,994·100% = 99,4%(- 0,6%).
Используя в качестве весов для изменений объема покупок удельный вес покупок в общей сумме затрат, получаем:
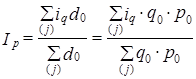(10.8)
т. е. индекс Iq - средний арифметический взвешенный из индивидуальных iq.
По данным нашего примера (табл. 10.3 и 10.4) общий индекс количества равен:
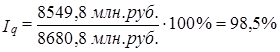
Получилось, что объем покупок продовольственных товаров сократился в среднем на 1,5%. Это более значительная оценка снижения, нежели полученная при расчетах по простой средней арифметической (- 0,6%). Так что мы еще раз получили подтверждение зависимости результата от использованной формулы.
Зная среднюю величину изменения показателя и индивидуальные индексы, можно проводить анализ методами вариационной статистики: анализировать распределение товаров по изменению цен, объема покупок, сравнивать модальное и среднее изменение, максимальное и минимальное; по показателям эксцесса распределений делать выводы о том, насколько однородны изменения цен и количества по отдельным товарам, группировать товары по уровню цен и степени их изменения и т. д.
Дата добавления: 2015-01-21; просмотров: 1023;