Ошибка выборки

Развитие современной теории выборочного наблюдения началось с простой случайной выборки.

В процессе проведения выборочного наблюдения, как и вообще при анализе данных любого обследования возникают ошибки. Все ошибки выборочного наблюдения подразделяются на ошибки выборки (случайные); ошибки, вызванные отклонением от схемы отбора (неслучайные) и ошибки наблюдения (случайные и неслучайные).

Ошибка отбора приводит к неслучайным ошибкам. Так бывает, если заменяется единицы, попавшие в выборку, другими единицами (например, если вместо отобранного домохозяйства, где в момент прихода исследователя никто не открыл дверь и был проведен опрос соседей, или когда появляются добровольные респонденты и просят, чтобы их опросили). Неслучайные ошибки возникают из-за методов сбора данных (неудобные вопросы, на которые не отвечают правдиво или неоднозначные по формулировке вопросы).

Случайные ошибки - это те ошибки, которые изменяются по вероятностным законам. К случайным относятся ошибки выборки.

В математической теории выборочного метода доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются.

Теоретической основой выборочного метода служат теоремы теории вероятностей П.Л. Чебышева и А.И. Ляпунова.

Теорема П.Л. Чебышева в приложении к выборочному методу формулируется следующим образом: «при неограниченном увеличении числа независимых наблюдений ( 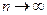) в генеральной совокупности с ограниченной дисперсией с вероятностью сколь угодно близкой к 1, можно ожидать, что отклонение выборочной средней 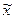от генеральной средней 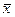будет сколь угодно мало, т.е. 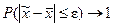при .

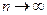Таким образом, теорема П.Л. Чебышева доказывает принципиальную возможность определения генеральной средней по данным простой случайной выборки.

Однако, пользуясь этой теоремой, мы не можем указать вероятность появления ошибок определенной величины. На этот вопрос отвечает теорема А.М. Ляпунова, доказанная в 1901 году. Согласно этой теореме при достаточно большом числе независимых наблюдений в генеральной совокупности с конечной средней и ограниченной дисперсией вероятность того, что 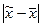(расхождение между выборочной средней и генеральной средней) не превзойдет по абсолютной величине некоторую величину tm равно интегралу Лапласа:

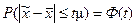, где Ф(t) – нормированная функция Лапласа.

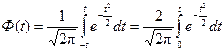(1)

Величина m - средняя квадратическая стандартная ошибка выборки.

Ошибка выборки или ошибка репрезентативности - это разница между значением показателя, полученного по выборке, и генеральным параметром. Так, ошибка репрезентативности выборочной средней равна 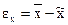, дисперсии .

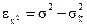Если предположить, что было проведено бесконечное число выборок равного объема из одной и той же генеральной совокупности, то показатели отдельных выборок образовали бы ряд возможных значений. Каждая выборка имеет свою ошибку репрезентативности. Эти ошибки также бы образовывали ряд. При бесконечно большом числе выборок получается кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используют для получения статистических заключений, установления вероятности той или иной величины, той или иной ошибки выборки.

По выборочному распределению может быть рассчитана средняя квадратическая ошибка репрезентативности:

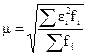
где ε²_i - квадрат ошибки выборки для i -той выборки;

f_i - число выборок с одинаковым значением выборочной средней.

Теперь выпишем среднее квадратическое отклонение выборочных средних от генеральной средней:

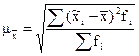
Эта формула называется средней ошибкой выборочной средней.

Поскольку, как правило, генеральная средняя 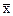неизвестна, этой формулой просто так нельзя воспользоваться. Кроме того, в социально-экономических исследованиях из одной и той же совокупности выборку не проводят многократно. Но можно воспользоваться методами теории вероятностей, основанными на использовании предельных теорем закона больших чисел. Для оценки ошибки выборки используют соотношение, которое вытекает из теоремы П.Л.Чебышева. Оно формулируется следующим образом: квадрат средней ошибки (дисперсия выборочных средних) прямо пропорциональна дисперсии признака х в генеральной совокупности σ² и обратно пропорциональна объему выборки n. Получаем следующую формулу:

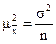
Следовательно, извлекая, квадратный корень, получаем среднюю ошибку выборочной средней.

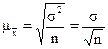
Таким образом, средняя ошибка выборки тем больше, чем больше вариация в генеральной совокупности, и тем меньше, чем больше объем выборки. Ошибка конкретной выборки может принимать различные значения, но отношение её к средней ошибке практически не превышает 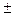3, если величина n достаточно большая (n>100).

Распределение ошибок выборочных средних имеет характер нормального распределения, даже если генеральная совокупность имеет иную форму распределения. Из формулы (5) получаем, что отклонение выборочной средней от генеральной средней равно:

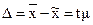
Эту формулу еще называют предельной ошибкой выборки

Нормированное отклонение t может быть установлено по таблице "Значение интеграла вероятностей". Для этого необходимо принять определенный уровень вероятности суждения о точности данной выборки. Вероятность, которая принимается при расчете ошибки выборочной характеристики, называется доверительной. Чаще всего принимают доверительную вероятность равной 0,95, 0,954 и 0,997 или даже 0,999. Доверительный уровень 0,95 означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы; вероятность 0,954 - в 46 случаях из 1000, при 0,997 - в 3 случаях из 1000, а 0,999 - в 1 случае из 1000. Коэффициент t – коэффициентом доверия.

Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения t для выборок достаточно большого объема (n≥30):

Чтобы вычислить ошибку выборки при принятой доверительной вероятности, нужно рассчитать величину средней ошибки 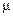. Формула (4) включает дисперсию признака в генеральной совокупности σ², которая, как правило, неизвестна. Доказано, что соотношение между σ² и σ 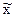² определяется следующим равенством: (следствие теоремы Чебышева)

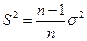
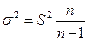
Если n велико то сомножитель n/(n-1) ≈1 и можно принять выборочную дисперсию в качестве оценки величины генеральной дисперсии. Подставляем выражение (10) в формулу средней ошибки выборки получим,

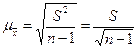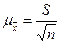или (9)

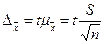
Ошибка выборки для выборочной относительной величины (доли) определяется аналогично. Дисперсия относительной величины по данным выборки: 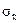² = w(1-w), где р- доля тех или иных единиц в выборке.

Средняя ошибка выборочной доли определяется по формуле:

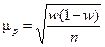
Предельная ошибка выборочной доли с принятой доверительной вероятностью имеет вид:

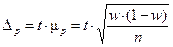(12)

При проведении выборочного наблюдения используются разные способы формирования выборочной совокупности: случайный отбор - повторный или бесповторный, механический, серийный и типический. Вид выборки влияет на величину ошибки. Мы с вами разобрали какова будет ошибка при случайном повторном (отбор единицами). При бесповторном отборе формула средней ошибки умножается на 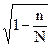, который корректирует величину ошибки выборки в связи с изменением состава совокупности и вероятности попадания единиц в выборку. Представим все формулы средней ошибки выборки в таблице:

Вид выборки	Средняя ошибка
выборочной средней	выборочной относительной (доли)
Повторная - отбор единицами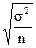
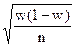
Бесповторная - отбор единицами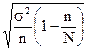
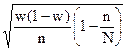
Серийная (нерайонированная)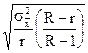
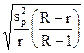
Районированная - отбор единицами, бесповторная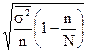
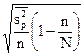
Районированная - отбор сериями, бесповторная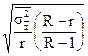

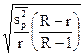
Здесь r - число отобранных серий, R - общее число серий. В серийной выборке дисперсия определяется как колеблемость между сериями по формуле:

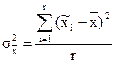(13)

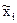- среднее значение признака х в i-той серии;

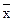- среднее значение в целом по выборке;

r - число отобранных серий.

Если серии не равны по числу единиц, то в числитель добавляется вес - число единиц i-той серии, а в знаменателе вместо к указывается ∑f_i.

При типическом отборе (районированная выборка) дисперсия рассчитывается как средняя из внутренних дисперсий:

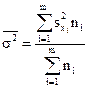(14)

где 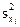- выборочная дисперсия признака х в i-том районе;

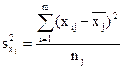(15)

n_j - объем выборки в j-том районе;

m - число районов.

При нерайонированной серийной выборке дисперсия рассчитываем по следующей формуле:

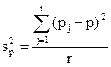(16)

где p_j - доля единиц определенной категории в j-той серии;

p - доля единиц этой категории в выборке.

При районированной серийной выборке дисперсия представляет среднюю из межсерийных дисперсий для каждого района:

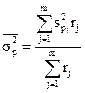(17)

где 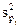- межсерийная дисперсия доли в j-том районе;

r_j - число серий, отобранных в j-том районе

m - число районов.