Парная регрессия на основе метода наименьших квадратов и метода группировок.

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:

прямой :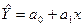

параболы - ;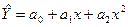

гиперболы -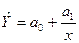

Определить тип уравнения можно, исследуя зависимость графически или аналитически: если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то связь - линейная, а при обратной связи - гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результативный - значительно быстрее, то используется параболическая, или степенная регрессия.

Оценка параметров уравнения регрессии (а₀, а₁, а₂) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Будем считать, что две величины Х и У взаимосвязаны между собой, причем У находится в некоторой зависимости от Х, т.е. У - зависимая величина, а Х - независимая.

Сущность метода заключается в нахождении параметров (а₀, а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению:

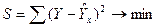
Для прямой зависимости:

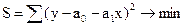
Рассматривая S в качестве функции параметров а₀, а₁ и продифференцируя по а₀ и по а₁ получаем систему уравнений:

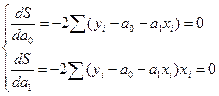
Отсюда система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:

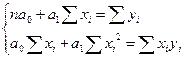
где n - объем исследуемой совокупности (число единиц наблюдения)

В уравнениях регрессии параметр а₀ показывает усредненное влияние на результативный признак неучтенных (невыделенных для исследования) факторов, параметр а₁ (в уравнениях параболы и а₂) показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

На практике часто исследования проводятся по большому числу наблюдений. В этом случае исходные данные и по факторному Х, и по результативному У признаку, т.е. уравнение парной регрессии целесообразно строить на основе сгруппированных данных. Если значения признаков Х и У заданы в определенных интервалах, то для каждого интервала сначала определяют середину интервала, а затем уже строят уравнение регрессии. В этом случае система нормальных уравнений регрессии примет вид:

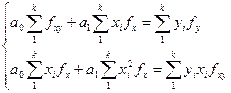
где k - число групп,

f_x, f_y - число единиц по факторному и результативному признаку по каждой группе;

Yf_y, Xf_x - значения результативного и факторного признаков по конкретной группе;

f_xy – частота повторения данного сочетания значений x и y.

Если связь нелинейная и описывается уравнением параболы второго порядка, то

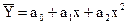
В данном случае задача сводится к определению неизвестных параметров а₀, а₁, а₂

Значения величин Х и У представлены двумя рядами данных:

У₁ У₂ У₃ … У_n

X₁ X₂ X₃ … X_n

Если бы все значения, полученные по данным наблюдениям лежали бы на строго на кривой, то для них было бы справедливо равенство:

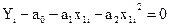
Однако на практике имеем отклонение эмпирических данных и теоретических:

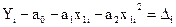
где 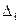- разность между данными наблюдения и данными, полученными по уравнению связи.

Можно минимизировать сумму квадратов отклонений, т.е. оценка ошибки по методу наименьших квадратов:

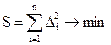
Метод наименьших квадратов обладает тем замечательным свойством, что делает число нормальных уравнений равным числу неизвестных коэффициентов. Приведенное уравнение параболы второго порядка имеет три неизвестных коэффициентов а₀, а₁, а₂. Следовательно, применяя метод наименьших квадратов, мы получим уравнение:

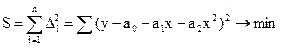
Для нахождения коэффициентов продифференцируем данное уравнение и приравняем частные производные к нулю, т.е.

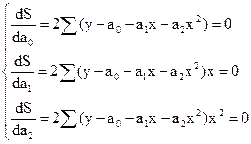
Проделав преобразования, получаем систему нормальных уравнений:

Решив систему этих уравнений, найдем значения неизвестных коэффициентов а₀, а₁, а₂ и получим уравнение регрессии.

Оценка обратной зависимости между Х и У может быть осуществлена на основе уравнения гиперболы:

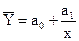
Проделав аналогичные рассуждения (как в линейной регрессии) для нахождения параметров гиперболы, можно получить систему уравнений:

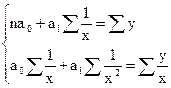
Решение вопроса о возможности использования метода наименьших квадратов для изучения связей между явлениями зависит от свойства оценок, получаемых с помощью этого метода. Даже при сравнительно небольшом числе наблюдений применение метода наименьших квадратов позволяет получить достоверные оценки. Этот метод может также использоваться в случаях проведения анализа косвенных наблюдений, являющихся функциями многих неизвестных.