Оценка тесноты связи.
Измерение тесноты и направления связи между признаками предлагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторов.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. 19 века Пирсоном, Эджвортом и Велдоном и характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В расчете этого коэффициента учитывается величина отклонений индивидуальных значений признаков от средней величины: 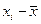 и
и 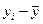 . Однако, сопоставляемые полученные величины могут быть выражены в различных единицах измерения или могут различны по величине. Поэтому сравнивают нормированные отклонения:
. Однако, сопоставляемые полученные величины могут быть выражены в различных единицах измерения или могут различны по величине. Поэтому сравнивают нормированные отклонения:
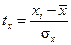 и
и 
Для получения обобщающей характеристики тесноты связи берут среднее произведение нормированных отклонений:
 (1)
(1)
Формула линейного коэффициента корреляции может быть представлена в следующем виде:
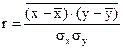
Используя математические свойства средней, получаем:
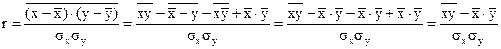 (2)
(2)
Преобразования данной формулы позволяют получить следующую формулу линейного коэффициента корреляции:
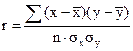 или
или 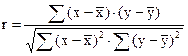 (3)
(3)
где n - число наблюдений
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
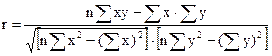 (4)
(4)
или
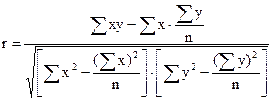 (5)
(5)
Коэффициент корреляции может быть выражен через дисперсии слагаемых:
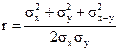 (6)
(6)
Формулы (1), (2), (2) применяются при изучении совокупностей малого объема (n<=20:30).
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
для парной корреляции - 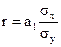 или
или 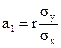 , а коэффициент
, а коэффициент 
для многофакторной корреляции - 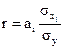 где аi - коэффициент регрессии в уравнении связи, σхi - среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака.
где аi - коэффициент регрессии в уравнении связи, σхi - среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака.
Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Линейный коэффициент корреляции изменяется в пределах от -1 до 1. При этом оценку линейного коэффициента корреляции можно представить в таблице:
| Значение линейного коэффициента корреляции | Характер связи | Интерпретация связи |
| r=0 | Отсутствует | - |
| 0 < r < 1 | Прямая | С увеличением Х увеличивается У |
| -1 < r < 0 | Обратная | С увеличением Х уменьшается У, и наоборот |
| r=1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
По степени тесноты связи различают количественные критерии оценки тесноты связи на основе шкалы Чеддока:
| Величина коэффициента корреляции при наличии | Характер связи | |
| прямой связи | обратной связи | |
| от 0,1 до 0,3 | от -0,3 до -0,1 | практически отсутствует |
| от 0,3 до 0,5 | от -0,5 до -0,3 | слабая |
| от 0,5 до 0,7 | от -0,7 до -0,5 | умеренная |
| от 0,7 до 0,9 | от -0,5 до -0,7 | сильная |
| 0,9 до 0,99 | от -0,99 до -0,9 | весьма сильная |
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношениерассчитывается по данным группировки, когда δ2 характеризует отклонения групповых средних результативного показателя от общей средней:
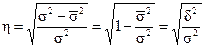 (7)
(7)
где η - корреляционное отношение;
σ2 - общая дисперсия
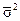 - средняя из частных (внутригрупповых) дисперсий;
- средняя из частных (внутригрупповых) дисперсий;
 - межгрупповая дисперсия (дисперсия групповых средних)
- межгрупповая дисперсия (дисперсия групповых средних)
Теоретическое корреляционное отношение определяется по формуле:
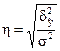 (8)
(8)
где 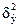 - дисперсия выровненных значений результативного признака, т.е. рассчитанных по уравнению регрессии;
- дисперсия выровненных значений результативного признака, т.е. рассчитанных по уравнению регрессии;
σ2 - дисперсия эмпирических (фактических) значений результативного признака.
Так как 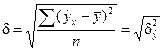 и
и 
Тогда 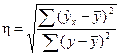 (9)
(9)
В основе расчета корреляционного отношения лежит правило сложения дисперсий, при этом средняя из межгрупповых дисперсий отражает вариацию результативного признака У под влиянием всех неучтенных при анализе факторов, т.е. носит остаточный характер. Поэтому её часто называют остаточной дисперсией.
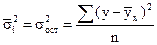
Отсюда формула корреляционного отношения принимает вид (выражаем межгрупповую дисперсию через общую и среднюю из внутригрупповых):
 (10)
(10)
Корреляционное отношение изменяется в пределах от 0 до 1 и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции. Теоретическое корреляционное отношение также может выражаться по формуле:
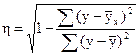
Корреляционное отношение является более универсальным показателем тесноты связи сравнению с линейным коэффициентом корреляции.
Для измерения тесноты связи при множественной корреляционной зависимости, т.е. при исследовании трех и более признаков одновременно, вычисляются множественный или совокупный и частные коэффициенты корреляции.
Множественный коэффициент корреляции рассчитывается при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.
В случае оценки связи между результативным (У) и двумя факторными признаками (х1 и х2) множественный коэффициент корреляции определяют по формуле:
 (11)
(11)
где r - парные коэффициенты корреляции между признаками
Множественный коэффициент корреляции можно рассчитать, используя парные коэффициенты rij и коэффициенты регрессии в стандартизованном масштабе (βi)
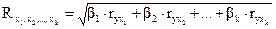
где ryxi - парные коэффициенты;
βi - коэффициенты в стандартизованном масштабе.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен.
Приближение R к 1 свидетельствует о сильной зависимости между признаками.
Чтобы оценить общую вариацию результативного признака в зависимости от факторных признаков, величина коэффициента множественной корреляции корректируется на основании следующего выражения:
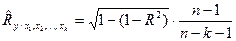
где 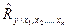 - скорректированное значение;
- скорректированное значение;
n- число наблюдений;
k - число факторных признаков.
Корректировка не производится при условии, если
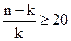
Проверка значимости коэффициента множественной корреляции осуществляется на основании F-критерия Фишера-Снедекора
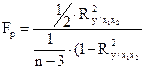
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других (к‑2) факторных признаков, т.е. когда влияние х3 и других исключается и оценивается связь между х1 и х2 в "чистом виде".
Коэффициент, в котором исключается влияние только одного факторного признака, называется коэффициентом частной корреляции первого порядка. В общем виде коэффициент корреляции первого порядка выражается так:
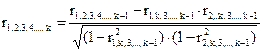
В случае зависимости Y от двух факторных признаков х1 и х2 коэффициент частной корреляции следующий:
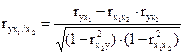
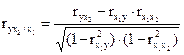
В первом случае исключено влияние факторного признака х2 , во втором - х1. Значения парного и частного коэффициентов корреляции отличаются друг от друга, так как парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный учитывает наличие и влияние других факторов.
Кроме перечисленных выше коэффициентов для измерения тесноты применяются коэффициент детерминации. Он равен квадрату корреляционного отношения и обозначается буквой η2
В числителе формулы стоит сумма квадратов отклонений фактических значений признака у от индивидуальных расчетных показателей. Эта сумма не может равняться нулю, если связь не является функциональной. При неверной формуле или ошибки в расчетах возрастают расхождения фактических и расчетных значений, и корреляционное отношение снижается.
С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле:
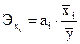
где 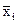 - среднее значение соответствующего факторного признака;
- среднее значение соответствующего факторного признака;
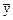 - среднее значение результативного признака;
- среднее значение результативного признака;
аi - коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько в среднем изменится значение результативного признака при изменении факторного признака на 1%.
Частный коэффициент детерминациипоказывает на сколько процентов вариация результативного признака объясняется вариацией i-того признака, входящего в множественное уравнение регрессии и определяется по формуле:
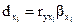
где ryxi - парный коэффициент корреляции между результативным и i-м факторным признаками;
βхi - соответствующий коэффициент уравнения множественной регрессии в стандартизованном виде.
Множественный коэффициент детерминации (R2) представляет собой множественный коэффициент корреляции в квадрате и показывает какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель.
Для более точной оценки влияния каждого факторного признака на моделируемый используют Q-коэффициент, определяемый по формуле:
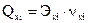
где 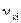 - коэффициент вариации соответствующего факторного признака.
- коэффициент вариации соответствующего факторного признака.
Интерпретировать корреляционные показатели строго следует лишь в терминах вариации отклонений от средней величины. Если же необходимо измерение изменений признака во времени, то метод корреляционно-регрессионного анализа требует значительного изменения. Модели на основе этого метода обладают слабыми экстраполяционными свойствами и не отражают тенденции развития и пригодны лишь для построения краткосрочных прогнозов.
Дата добавления: 2015-03-03; просмотров: 5225;
