Проверка значимости параметров регрессии.

Проверка статистической значимости всех параметров, полученных в процессе корреляционно-регрессионного анализа, основывается на предположении, что все эти параметры, а точнее, их значения являются конкретными числовыми реализациями некоторых случайных величин. И для каждого конкретного значения параметра можно оценить как вероятность превышения найденной величины, так и вероятность того, что в процессе расчета могли получить меньшее значение параметра. Здесь используется принцип практической невозможности маловероятных событий. Если найденная величина параметра все-таки попала в зону маловероятных значений, то с достаточной для практики строгостью данное значение параметра можно считать неслучайным или статистически значимым. Если же конкретное значение параметра попадает в область весьма вероятных значений, то это говорит о случайности вычисленного параметра,, его статистической незначимости - доверие к такому параметру уменьшается. Проверка значимости сводится к сравнению полученного значения с тем числом, которое отделяет область маловероятных значений от весьма вероятных.

В настоящее время большинство расчетов по корреляционно-регрессионному анализу выполняется с помощью пакетов прикладных программ по статистике. Соответствующие пакеты обеспечивают такую проверку, сообщая граничную величину t-критерия Стьюдента и (или) F-критерия Фишера.

Для парной регрессии значения критериев определяются следующим образом.

Значимость линейного коэффициента корреляции r и параметров a₀ и а₁ в уравнении Y=a₀+a₁X оценивается на основе t-критерия Стьюдента

значимость параметра а₀ определяется из уравнения

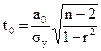
Для оценки значимости уравнения регрессии в целом, особенно при нелинейных зависимостях, используют F-критерий:

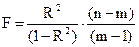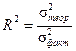, где и носит название индекса детерминации.

где m - число параметров уравнения регрессии (число линейных уравнений, по которым определялись параметры уравнения регрессии)

Расчетное значение t-критерия сравнивается по абсолютной величине с граничным (табличным) значением распределения Стьюдента при (n-m) степенях свободы и заданном уровне значимости (чаще всего принимают α=0,01 или α=0,05). Если фактическое значение t-критерия больше табличного, то данный параметр считается значимым. Аналогично сравнивается с табличным расчетное значение F-критерия при заданном уровне значимости α и k₁ = n-m степенях свободы.

При проверке значимости эмпирического корреляционного отношения m - число групп, выделенных в процессе группировки по факторному признаку, а вместо R² в формулу F-критерия подставляют величину η².

При анализе уравнений множественной регрессии - линейной и нелинейной - возникает задача отбора наиболее значимых признаков-факторов Х. Признак Х считается значимым, если соответствующий параметр регрессии по абсолютному значению настолько отклонился от своего предполагаемого нулевого среднего уровня, что произошло событие редкое, маловероятное. В этом случае и параметр a_i и признак Х_i признается статистически значимым. Степень отклонения оценивается t-критерием, т.е.

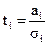, i=0,1,2,…,k

где а_i - численное значение i-го параметра уравнения множественной регрессии; σ_i - среднее квадратическое отклонение параметра а_i (как случайной величины) относительно нулевого уровня. Наиболее трудоемкой в техническом отношении оказывается оценка σ_i , если расчеты производятся с помощью пакетов прикладных программ, то это значение высчитывается автоматически, после чего они сравниваются с табличным уровнем t при определенной значимости α и (n-m) степенях свободы, где n - число наблюдений, а m - число параметров уравнения регрессии.