Методы выявления типа тенденции динамики. Ряд динамики может быть подвержен влиянию различных факторов
Ряд динамики может быть подвержен влиянию различных факторов. Под действием эволюционных факторов происходят изменения, которые определяют общие направления развития, называемые тенденцией или трендом.
Влияние циклических, сезонных факторов приводят к колебаниям, т.е. отклонениям от основной тенденции. Тренд – это долговременная компонента ряда динамики, которая характеризует основную тенденцию его развития.
Прежде чем перейти к выделению тренда и построению его уравнения, следует проверить гипотезу о том, существует ли он вообще. Отсутствие тренда означает неизменность среднего уровня ряда во времени. В настоящее время существует около 10 критериев для проверки наличия тренда. Рассмотрим два из них: метод, основанный на проверке разности средних двух разных частей одного и того же ряда, и метод Фостера-Стьарта.
Проверка существенности разности средних. Ряд динамики разбивают на две равные или почти равные части. Проверяется гипотеза о существовании разности средних: Н0 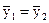 . За основу берется критерий Стьюдента. При t > tкрит гипотеза об отсутствии тренда отвергается, при t < tкрит гипотеза принимается. Здесь t расчетное значение, найденное для анализируемых данных, tкрит – табличное значение этого критерия при уровне значимости a.
. За основу берется критерий Стьюдента. При t > tкрит гипотеза об отсутствии тренда отвергается, при t < tкрит гипотеза принимается. Здесь t расчетное значение, найденное для анализируемых данных, tкрит – табличное значение этого критерия при уровне значимости a.
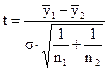 где
где
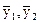 - средние для первой и второй половины ряда;
- средние для первой и второй половины ряда;
n1 , n2 – число наблюдений в этих частях ряда;
s - среднее квадратическое отклонение разности средних.
Значение tкрит берется с числом степеней свободы, равным n1+n2-2. Необходимое значение s может быть определено на основе средневзвешенной величины дисперсий отдельных совокупностей:
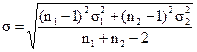 где
где
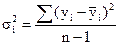
Следует заметить, что данный метод дает хорошие результаты лишь в случае рядов с монотонной (постоянной) тенденцией. Когда же ряд динамики меняет общее направление, то точка поворота тенденции оказывается близкой к середине ряда, поэтому средние двух отрезков будут близки и проверка может не показать наличие тенденции.
Метод Фостера-Стьдента Расчет состоит из следующих этапов:
1. Сравнивается каждый уровень ряда со всеми предыдущими, при этом
если 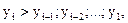 то
то 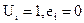
при 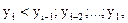 то
то 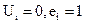
если же одно из неравенств не выполняется, то 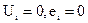
2. Вычисляются значения величин S и d по формулам:
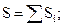
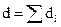 , где
, где
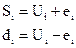
Показатель S может принимать значения 0<=S<=n-1, причем S=0, когда все уровни равны между собой и S=n-1, когда ряд динамики монотонно возрастает или убывает. Показатель d характеризует изменение тенденции в среднем.
3. Проверяется с использованием t-критерия Стьюдента гипотеза о том, можно ли считать случайными разности S-m и d-0:
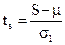 ; и
; и 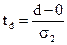
где m - среднее значение величины S, для ряда, в котором уровни расположены случайным образом
s1 – стандартная ошибка величины S
s2 – стандартная ошибка величины d
Значения величин m, s1, s2 – табличные и приводятся в специальных таблицах.
4. Сравниваются расчетные величины ts и td с табличными из распределения Стьюдента при заданной вероятности a. Если ts<tтабл и td< tтабл, то гипотеза об отсутствии тренда в средней величине и дисперсии подтверждается.
Дата добавления: 2015-03-03; просмотров: 1043;
