Определение необходимой численности выборки.

Средняя квадратическая (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности. Уменьшение стандартной ошибки выборки, а следовательно увеличение точности оценки, всегда связано с увеличением объема выборки. В этой связи уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Рассмотрим формулу предельной ошибки выборки для случая простой случайной повторной выборки:

,

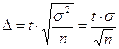Отсюда

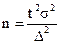(18)

где ∆ - допустимая погрешность, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;

t - табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;

σ² - генеральная дисперсия.

При проектировании выборочного наблюдения предполагается заранее заданной величина предельной допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения (коэффициент доверия t соответствует принятому уровню доверительной вероятности).

Генеральная дисперсия, как правило, неизвестна. Поэтому используются приближенные способы ее оценки: результаты прошлых обследований той же совокупности, если её структура и условия развития достаточно стабильны, или же зная примерную величину средней, находят дисперсию из соотношения σ ≈⅓ х.

Если распределение признака в генеральной совокупности приближается к нормальному распределению и известны х_max и x_min , то можно определить среднее квадратическое отклонение в соответствии со следующим правилом (называемом правилом трех сигм) σ = 1/6 (х_max - x_min), так как в нормальном распределении в размахе вариации 6 σ. Если распределение заведомо ассиметричное, то для него σ ≈ 1/5(х_max - x_min).

При расчете n не следует брать слишком большое значение t и малым значением ∆, так как это приводит к увеличению объема выборки, а следовательно, к увеличению затрат и времени.

Формула (18) не учитывает бесповторную выборку и дает максимальную величину выборки, которую можно скорректировать, учитывая "бесповторность"

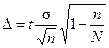(19)

и выражая отсюда n, получаем выражение скорректированного объема выборки

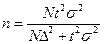(20)

При проектировании типической выборки рассчитанный объем выборки распределяют пропорционально численности районов (пропорциональный отбор):

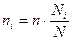(21)

где n_i - объем выборки для i-го района;

N_i - объем i-го района в генеральной совокупности;

n - общий объем выборки;

N - общий объем генеральной совокупности

При различиях в однородности выделенных районов лучшие результаты дает распределение запланированного объема выборки между районами с учетом дисперсии признака (оптимальный отбор). В этом случае объем выборки в i-том районе определяется как

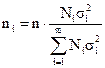(22)

где σ_i² - дисперсия признака х в i-том районе.

После проведения выборки рассчитывают возможные ошибки выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для изучения характеристик генеральной совокупности.

Выборочные средние и относительные величины распространяют на генеральную совокупность обязательно с учетом предела их возможной ошибки. Чаще всего указывают границы значений генеральной характеристики с определенной вероятностью F(t):

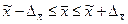
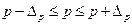
Иногда указывают только один (верхний или нижний) предел характеристики генеральной совокупности.

На основе выборки могут быть получены и значения объемных показателей, т.е. подсчетов для генеральной совокупности. Такой расчет осуществляется 2 способами: путем прямого расчета и способом коэффициентов. Прямой расчет заключается в том, что выборочная средняя или доля умножается на объем генеральной совокупности:

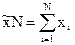(25)

Так как средняя величина имеет ошибку выборки 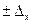, то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах

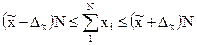(26)

Итоговый подсчет по генеральной совокупности можно получить на основе итогового под счета по выборке, разделив его на долю единиц совокупности:

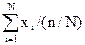(27)

При способе коэффициентов используются не только выборочные данные, но и сведения о генеральной совокупности. Этот способ основан на связи признаков друг с другом. Например, в результате выборочного наблюдения семей города получены размер среднедушевого дохода ( 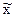), средний доход семьи ( 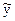), среднее число человек в семье 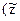). Так что 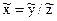. Зная численность города, требуется рассчитать общую величину денежного дохода населения. Очевидно, что это можно сделать, умножив душевой доход на общее число жителей в городе: 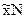. Общий доход можно получить, суммируя доход отдельных семей; численность населения можно получить, суммируя данные о числе членов семей. Тогда

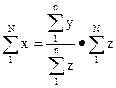(28)

Средний душевой доход представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Перегруппируем множители в данной формуле и получим:

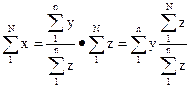(29)

Последний сомножитель, не что иное, как обратная величина доли отбора, рассчитанной по значениям признака z.

Итак, итоговый подсчет по генеральной совокупности может быть получен делением соответствующего итогового подсчета по выборке на долю отбора. При прямом расчете берется доля отбора единиц совокупности, при способе коэффициентов - доля отбора по значению какого-либо признака.