Показатели размера и интенсивности вариации.
Абсолютные средние размеры вариации. Следующим этапом изучения вариации признака в совокупности является измерение характеристик величины вариации. Простейшим из них служит размах или амплитуда вариации - разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений. Таким образом, размах вариации вычисляется по формуле:
R = xmax - xmin
Но эта величина не может служить для обобщения всех различных значений признака. Для этих целей служит показатель, который называется средний модуль отклонений или среднее линейное отклонение:
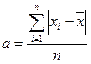
Для дискретных и интервальных рядов среднее линейное отклонение вычисляется как взвешенное по частоте отклонение, т.е. по формуле:
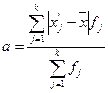
Для нашего примера с урожайностью это составит а= 980,2 : 143 = 6,85 ц/га. Это означает, что в среднем урожайность в изучаемой совокупности хозяйств отклонялась от средней урожайности по области на 6,85 ц/га. Простота расчета и интерпретации составляет положительные стороны данного показателя, однако с математической точки зрения модуль нельзя поставить в соответствие каким либо вероятностным законам. Самый простой выход - возвести все отклонения во вторую степень. Оказалось, что обобщающие показатели вариации, найденные с использованием вторых степеней обладают замечательными свойствами. Поэтому они получили широкое распространение, на их основе были разработаны новые методы исследования, а также новые показатели количественной характеристики большого класса явлений. Полученная величина называется дисперсией (σ2), а корень квадратный из дисперсии - среднее квадратичное отклонение, которое обозначают малой строчной греческой буквой σ (сигма) по формуле
Для ранжированного ряда:
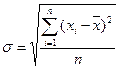
для интервального ряда:
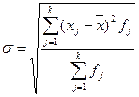
Дисперсия. Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия σ2, определяемая как квадрат среднего квадратичного отклонения, измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Формула дисперсии:
простая (для несгруппированных данных):
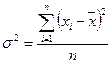
и взвешенная (для сгруппированных данных):
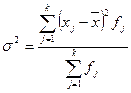
Дисперсия обладает следующими свойствами:
Свойство 1. Дисперсия постоянной величины равна 0
Свойство 2. Уменьшение всех значений признака на одну и туже величину А не меняет величины дисперсии:
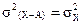
Значит, средний квадрат отклонения можно вычислить не по заданным значениям признака, а по отклонениям их от какого-то постоянного числа.
Свойство 3. Уменьшение всех значений признака в k раз уменьшает дисперсию в k2 раз, а среднее квадратичное отклонение в k раз:

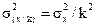
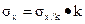
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение достигается посредством вычисления и анализа различных видов дисперсии. Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов.
Межгрупповая дисперсия (δ2) характеризует различия в величине изучаемого признака, возникающие под воздействием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:

где к – число групп;
nj – число единиц в j-группе;
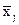 - средняя величина в j-группе;
- средняя величина в j-группе;
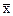 - средняя величина по совокупности единиц.
- средняя величина по совокупности единиц.
Внутригрупповая дисперсия (σ2i) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
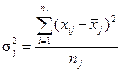
т.е. определяем дисперсию в каждой группе совокупности.
По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из всех внутригрупповых дисперсий:
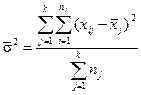
Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из групповых и межгрупповой дисперсий:
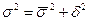
Данное отношение называют правилом сложения дисперсий. Согласно этого правила, общая дисперсия, возникающая под воздействием всех факторов, равна сумме дисперсии, появляющейся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
На дисперсии основаны практически все методы математической статистики.
Для оценки интенсивности вариации и для сравнения её в разных совокупностях и тем более разных признаков необходимы относительные показатели вариации. Они получаются делением абсолютных показателей на среднюю арифметическую величину признака. Получаем следующие показатели:
1) относительный размах вариации ρ:
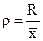
Дата добавления: 2015-03-03; просмотров: 1539;
