Средняя квадратическая величина

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться средней квадратической величиной (х_кв). Её формула такова:

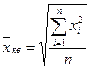- простая (для негруппированных данных)

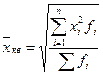- взвешенная (для группированных данных)

Например, имеются три участка земельной площади со сторонами квадрата х₁ = 100 м, х₂ = 200 м, х₃ = 300 м. Заменяя разные значения длины сторон на среднюю, мы очевидно, должны исходить из сохранения общей площади всех участков. Арифметическая средняя величина (100 + 200 + 300) : 3 = 200 м не удовлетворяет этому условию, так как общая площадь трех участков со стороной 200 м была бы равна: 3 * (200м)² = 120 000м² . В то же время площадь всех исходных участков равна: (100 м)² + (200 м)² + (300 м)² = 140 000 м². Правильный ответ дает средняя квадратическая:

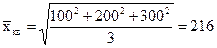м

Далее мы с вами будем изучать изменения вариации признака в совокупности. И там главной сферой применения средней квадратической является именно вычисление этого изменения.

Аналогично. Если необходимо сохранить неизменной сумму кубов индивидуальных значений признака при замене на среднюю величину, используют среднюю кубическую, которая определяется следующим образом

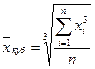- простая (для негруппированных данных)

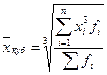- взвешенная (для группированных данных)