Виды средней арифметической
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимаются середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. Например, у нас есть данные о распределении рабочих предприятия по возрасту:
Распределение рабочих предприятия по возрасту
| Группы рабочих по возрасту, лет | Число рабочих fi | Середина интервала х'i | xifi |
| До 20 | 18,5 | ||
| 20-30 | |||
| 30-40 | |||
| 40-50 | |||
| Старше 50 | 57,5 | ||
| Итого |
Рассмотрим первый интервал, логично считать. Что младше 17 лет вряд ли будут работать на предприятии, следовательно, первый интервал 0т 17 до 20 лет. Последний интервал логично выбрать 50 - 65 лет. Посчитаем середину интервала: (17+20):2 = 18,5. Аналогично высчитываем середину последнего интервала. Суммируем второй столбец и получаем число рабочих предприятия - 359. Далее заполняем последний столбец и суммируем итог - 12408. Теперь можно вычислить средний возраст рабочих по формуле средней взвешенной с заменой точных значений признака в группах серединами интервалов:
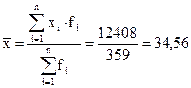
что можно и внести в итоговую строку таблицы.
Перейдем к рассмотрению средних вторичных (относительных) признаков. Сумма таких показателей сама по себе реальной величиной какого-либо признака в совокупности не является. Однако общее определение арифметической средней сохраняет силу и в этом случае. При вычислении таких средних величин необходимо, чтобы сохранялась сумма величины объемного признака, который является числителем при построении осредняемого относительного показателя. Например, при вычислении средней величины урожайности какой-либо культуры (по формуле (2)) необходимо, чтобы общий объем валового сбора этой культуры остался неизменным при замене индивидуальных величин урожайности средней величиной. Нельзя менять реальную величину объемного признака - она является базой расчета средней. Чтобы выполнить указанное условие, в качестве весов при расчете средней величины относительного показателя необходимо принять значение того признака, который является знаменателем при определении относительного показателя. Так, при вычислении средней урожайности по совокупности хозяйств весами должны быть размеры площади данной культуры.
Рассмотрим пример расчета средней доли предметов народного потребления в общем выпуске промышленной продукции по совокупности предприятий, представленных в таблице:
| Номера предприятий | Объем всей продукции, млн. руб., fi | Доля товаров народного потребления, % xi | Объем выпуска товаров народного потребления, млн. руб., хifi |
| 103,5 | |||
| 247,0 | |||
| 124,8 | |||
| 140,2 | |||
| Итого | 615,5 |
В этом случае весом должна быть общий объем всей продукции предприятия. Тогда средняя доля предметов народного потребления в продукции четырех предприятий равна: 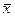 = (615,5 : 2047) * 100% = 30,07 %. Теперь эти цифры можно внести в соответствующую графу таблицы. Числитель средней величины ∑хi fi - это объем выпуска предметов потребления всеми предприятиями - величина, которая должна сохраняться неизменной при замене разных четырех долей на среднюю долю. Расчет по данным таблицы проведен на основе известных индивидуальных значениях усредняемого признака.
= (615,5 : 2047) * 100% = 30,07 %. Теперь эти цифры можно внести в соответствующую графу таблицы. Числитель средней величины ∑хi fi - это объем выпуска предметов потребления всеми предприятиями - величина, которая должна сохраняться неизменной при замене разных четырех долей на среднюю долю. Расчет по данным таблицы проведен на основе известных индивидуальных значениях усредняемого признака.
 Однако исходная информация может иметь другую форму: индивидуальные значения усредняемого признака могут быть неизвестны, зато известны индивидуальные или суммарные значения объемных признаков как числителя, так и знаменателя относительной величины. Например, известно, что в акционерном сельскохозяйственном предприятии было посажено 145 га картофеля и собрано с них 2595,5 т продукции. При этом совершенно неизвестно, сколько было собрано с каждого гектара из 145 га в отдельности, хотя на самом деле, конечно, индивидуальные величины существовали объективно. Однако никакой потребности в их раздельном учете нет; учет продукции ведется по бригадам, по отдельным полям севооборота, но не по каждому гектару. Среднюю урожайность картофеля получают попросту делением массы собранного продукции на площадь посадки, т.е. как относительную величину, характеризующее хозяйство в целом:
Однако исходная информация может иметь другую форму: индивидуальные значения усредняемого признака могут быть неизвестны, зато известны индивидуальные или суммарные значения объемных признаков как числителя, так и знаменателя относительной величины. Например, известно, что в акционерном сельскохозяйственном предприятии было посажено 145 га картофеля и собрано с них 2595,5 т продукции. При этом совершенно неизвестно, сколько было собрано с каждого гектара из 145 га в отдельности, хотя на самом деле, конечно, индивидуальные величины существовали объективно. Однако никакой потребности в их раздельном учете нет; учет продукции ведется по бригадам, по отдельным полям севооборота, но не по каждому гектару. Среднюю урожайность картофеля получают попросту делением массы собранного продукции на площадь посадки, т.е. как относительную величину, характеризующее хозяйство в целом:
Средняя урожайность = (валовой сбор, т)/(площадь посадки, га) = 2595,5/145= 17,9 т/га. По отношению к предприятию это относительный показатель. Но существуют и сами значения урожайности с каждого из 145 га, хотя и неучтенные. По отношению к ним 17,9 - это средняя величина. Такую форму определения средней арифметической называют неявной формой средней.
Дата добавления: 2015-03-03; просмотров: 992;
