Многомерные группировки

Группировка, осуществляемая одновременно по комплексу признаков называется многомерной. Характеристика одной и той же стороны изучаемого явления может быть дана с помощью набора признаков. Например, для характеристики технического уровня развития предприятий может быть использованы следующие показатели: удельный вес активной части промышленно-производственных основных фондов, удельный вес автоматических машин и оборудования в составе рабочих машин и оборудования, электровооруженность труда, машиновооруженность рабочих, коэффициент обновления машин и оборудования.

Характеризуя таким образом каждую единицу совокупности набором признаков, можно рассматривать эту единицу как точку в m-мерном пространстве, а задача многомерной группировки будет состоять в выделении точек, составляющих однородные группы единиц. Исходные данные для задачи многомерной группировки представляют в виде матрицы «объект-признак». Строками ее являются значения признаков, характеризующих соответствующий объект, а столбцами – значения каждого признака для рассматриваемой совокупности объектов.

Мерой «сходства» между единицами может служить различные критерии. В зависимости от выбранного критерия и существуют различные виды многомерной группировки.

Выделяют 3 типа мер сходства:

1. коэффициент подобия;

2. коэффициент связи;

3. показатели расстояния.

Меры первого и второго типов называют мерами близости: чем больше их величины, тем ближе объекты к друг другу.

Обратное положение с показателями расстояния: чем больше их величины, тем больше различия между объектами.

Меры сходства могут определяться как между объектами, так и между признаками.

Для измерения степени близости между парами объектов (i и j) используют коэффициенты подобия S. Один из наиболее простых способов рассчитать этот коэффициент по формуле:

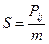, где Р_ij – число совпадающих признаков у объектов i и j, а m – общее число признаков, по которым осуществляется сравнение. Очевидно, что 0 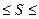1.

Часто в качестве мер сходства используют коэффициент корреляции – либо как измеритель силы связи между объектами (строками матрицы), либо как измерители связи признаков (столбцами матрицами).

Если признаки не поддаются точной количественной оценке, то мерами их связи служат коэффициенты ранговой корреляции.

Во многих случаях роль меры сходства играет функция расстояния. Для сопоставимости статистических показателей расстояния определяют по статистическим стандартизированным данным, т.е. заменяют первичные данные данными, вычисляемыми по формуле: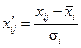

Чаще всего принимаются следующие меры расстояния между объектами:

1. хеммингово расстояние:

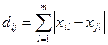
2. евклидово расстояние:

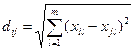
где x_il – значение l-го признака у объекта i

x_jl – значение l-го признака у объекта j

Евклидово расстояние не учитывает неравнозначность осей пространства. При ненормированных осях возможен случай, когда 2 объекта, сильно различающихся только по одному признаку, окажутся далекими в евклидовом пространстве. Поэтому часто вводят взвешенное евклидово расстояние, где подбором весов w_l пытаются нормировать оси пространства:

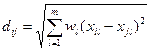, где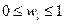

Обычно величину w_l - обратно пропорциональна среднему квадратическому отклонению σ значений признака х_l.

3. расстояние Махаланобиса:

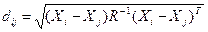
где X_i=( X_i1, … , X_im) – строки значений признаков для объекта i

X_j=( X_j1, … , X_jm) – строки значений признаков для объекта j

R^-1 – матрица, обратная матрице парных линейных коэффициентов корреляции признаков.

Применение методов многомерной группировки связано с большой вычислительной работой и осуществляется с помощью специальных алгоритмов, реализованных в различных статистических пакетах прикладных программ.

С помощью различных методов (дендроидов, метода шаров, корреляционных плеяд, многомерной средней, кластерного анализа) осуществляется формирование групп, в которых единицы совокупности объединяются на основании близости по всему комплексу признаков.