Значение и сущность группировки. Построение группировки

Изучаемые статистикой массовые явления и процессы протекают в множествах элементов (единиц) некоторого вида, или совокупностях. Определить совокупность – значит определить входящие в нее элементы, т.е. единицы. Структура совокупности показывает, как единицы разграничиваются друг с другом, т.е. под структурой понимается характер распределения единиц совокупности для каждого признака и характер взаимосвязи признаков между собой.

В простейших случаях явление протекает в одной совокупности. В более сложных в рамках самой совокупности существуют качественно различные частные совокупности, без разграничения которых невозможно разобраться в массовом явлении. Так, если единицей совокупности «Пищевая промышленность» является предприятие, то в составе предприятия действуют совокупности рабочих, станков. Состав совокупности по таким качественно различным частям, играющим разную роль в исследуемом массовом явлении, представляет собой одну из важнейших характеристик структуры этой совокупности.

Каждая совокупность должна объединять качественно однородные элементы, играющие в рассматриваемом массовом явлении вполне определенную роль. Игнорирование качественных различий ведет к грубым ошибкам.

В изучении массового явления необходимо, прежде всего, определить действующие в нем качественно однородные совокупности. Это первое основное требование научной методологии в статистике. Выделение и анализ однородных подсовокупностей выполняют с помощью методов группировки.

Таким образом, мы записываем определение. Группировка - это распределение единиц совокупности по группам в соответствии со следующим принципом: различия между единицами, отнесенными к одной группе, должны быть меньше, чем между единицами, отнесенными к разным группам.

Группировка лежит в основе дальнейшей работы с собранной информацией. На основе группировок рассчитываются сводные показатели по группам, появляется возможность их сравнения, анализа причин различий между группами, изучение взаимосвязей между признаками. Если рассчитывать сводные показатели только по совокупности в целом, то мы не сможем уловить её структуры, роли отдельных групп, их специфики.

Таким образом, значение группировки состоит в том, что этот метод обеспечивает обобщение данных, представление их в компактном виде. Кроме того, группировка создает основу для последующей сводки и анализа данных.

Сводные показатели для отдельных групп являются типичными и устойчивыми, если, во-первых, группировка проведена правильно, во-вторых, группы имеют достаточную численность. При достаточно большом числе единиц (не менее 5 в группе) в сводных показателях взаимопогашаются случайные характеристики и проявляются закономерные, типичные.

Для построения группировки необходимо установить правила отнесения каждой единицы к той или иной группе. Эти правила включают в себя, во-первых, определение группировочных признаков - это характеристики (признаки), по которым происходит объединение отдельных единиц совокупности в однородные группы. Его часто называют основанием группировки. Во-вторых, определить интервалы группировки, т.е. значение характеристик, которые будут отделять одну группу от другой.

В качестве основания группировки следует использовать существенные признаки. В каждом конкретно исследовании он будет свой, в зависимости от целей исследования.

В основании группировки могут быть положены как количественные, так и качественные признаки. Количественные имеют численное выражение (объем торгов, курс доллара в рублях, возраст человека, денежный доход семьи и т.д.), а качественные отражают состояние единицы совокупности (пол человека, его национальную принадлежность, семейное положение, отраслевая принадлежность предприятия, его форма собственности и организационно-правовая форма и т.д.)

После определения основания группировки следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность. Число групп зависит от задач исследования и вида признака, положенного в основание группировки, численности совокупности, степени вариации признака.

Единицы совокупности могут быть разбиты на разное число групп по одному и тому же признаку. Например, при группировке населения по возрасту с целью определения трудовых ресурсов страны все население в практической статистике делится на три группы: население моложе трудоспособного возраста, трудоспособное население и население старше трудоспособного возраста. Если же анализируется продолжительность жизни, то строится более детальная группировка, и выделяются пятигодичные группы.

При построении группировки по качественному признаку групп, как правило, будет столько, сколько будет градаций, видов, состояний у этого признака. Например, в случае проведении группировки населения по полу можно образовать только две группы: мужчины и женщины. Если проводится группировка производства товаров народного потребления по экономическим районам, то вся совокупность делится на 11 групп: именно на столько районов поделена территория страны.

При небольшом объеме совокупности не следует образовывать большое число групп, так как группы будут слишком малочисленны, что не позволит получить верные характеристики исследуемого явления. (Минимальное число единиц в группе должно быть не меньше 5).

Одним из способов определения числа групп является использование формулы Стерджесса. Мы говорили о ней при построении вариационных рядов. Эта формула имеет вид: k = 1 + 3,322 lg n, где к - число групп, n - число единиц совокупности. Мы видим, что выбор числа групп по этой формуле зависит от объема совокупности.

Недостатком этой формулы состоит в том, что её применение дает хорошие результаты, если совокупность состоит из большого числа единиц.

Другой способ основан на применении показателя среднего квадратичного отклонения (σ). Если принять величину интервала равной 0,5σ, то совокупность разбивается на 12 групп, а когда величина интервала равна 2/3σ и σ, то совокупность делится соответственно на 9 и 6 групп. Если 12 групп, то интервалы строятся следующим образом:

1 - 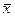- 3,0 σ 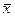- 2,5 σ

2 - 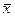- 2,5 σ 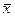- 2,0 σ

……………………………

7 - 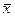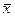+ 0,5 σ

8 - 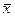+ 0,5 σ 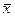+ 1,0 σ

………………………………

12 - 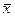+2,5 σ 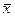+ 3,0 σ, где 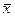среднее значение признака, определяемое как среднее арифметическое, σ - среднее квадратическое отклонение. Но все равно эти методы не дают гарантии в том, что не будут сформированы "пустые" или малочисленные группы. Наличие таких интервалов свидетельствует, что группировка построена неверно.

После определения числа групп следует определить интервалы группировки.

Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Интервалы бываю:

§ равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова;

§ неравные, когда например, ширина интервала постепенно увеличивается, а верхний интервал не закрывается вовсе;

§ открытые, когда имеется либо верхняя, либо нижняя граница;

§ закрытые, когда имеются и нижняя, и верхняя границы.

Интервал - это значение варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну их них. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в нем. Величина интервала - разность между верхней и нижней границами интервала.

Определение интервала группировки. Существует следующие виды интервалов - открытые и закрытые. Открытые интервалы - это интервалы, у которых указывается верхняя и нижняя граница. Например, группы предприятий по численности работающих человек: 200-600,600-100 и т.д. Эта запись предполагает, что единица, у которой значение признака совпадает с верхней границей, относится к следующей группе и интервал читается как "от - до". Если указана только верхняя или только нижняя граница, то интервал называют открытым. Например, до 200 человек или 2000 человек и более. Ширина открытого интервала принимается равной ширине смежного с ним интервала.

Закрытые интервалы подразделяются на равные и неравные. Величину равного интервала мы с вами рассматривали, когда строили вариационные ряды. Формула равного интервала:

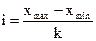, где к – число групп

Полученную величину округляют. Она является шагом интервала.

Если полученное число имеет один знак до запятой, то полученные значения округляют до десятых. Если величина имеет два знака до запятой, то округляют до целого числа.

Неравные интервалы применяются в статистике, когда значение признака варьируется неравномерно и в значительных размерах. Неравные интервалы могут определяться как равнонаполненные. При этом совокупность разделяется на группы равного объема с числом единиц равным 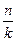, где n - общее число единиц, а k - число групп.

Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся по арифметической прогрессии, определяется по формуле:

i_k+1 = i_k+ a;

в геометрической прогрессии:

i_k+1 = i_k∙ q, где

а - константа - число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным при прогрессивно убывающих интервалах;

q - константа - положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих - меньше 1.

При определении границ интервалов статистических группировок исходят из того, что изменение количественного признака приводит к появлению нового качества. В этом случае граница устанавливается там, где происходит переход от одного качества к другому.

При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно возрастающими, ни прогрессивно убывающим. Такие интервалы называют произвольными. Например, при переписи населения 1989 года для группировки семей и одиночек по размеру жилой площади, приходящейся на одного человека, применялись следующие группы (м²): до5; 5-6; 7-8; 9-12; 13-14; 15-19; 20 и более. Произвольные интервалы часто используют при группировки рабочих по выработке продукции, предприятий по уровню рентабельности.

Группировка с произвольным интервалами может быть построена с помощью коэффициента вариации, определяемого по формуле ν = 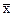: σ.

Построение группировки этим методом начинается с упорядочения единиц совокупности по возрастанию или убыванию группировочного признака. В полученном ряду значений признака его значения объединяют в группу до тех пор, пока исчисленный для этой группы коэффициент вариации не станет, равен 33%. Это будет свидетельствовать об образовании первой группы, которая исключается из совокупности. Оставшаяся её часть принимается за новую совокупность, для которой повторяется алгоритм образования новой группы. Итак, до тех пор, пока все единицы совокупности не будут объединены в группы.