Основные виды графиков
Иногда статистические таблицы дополняются графиками, когда ставится цель подчеркнуть какую-то особенность данных, провести их сравнение. Графики являются самой эффективной формой представления данных с точки зрения их восприятия. Часто графики используются и вне связи с таблицей. С помощью графиков достигается наглядность характеристики структуры, динамики, взаимосвязи явлений, их сравнения.
Статистические графики представляют собой условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или географических карт-схем.
На графике сразу видны пределы изменения показателя, сравниваемая скорость изменения разных показателей. Вместе с тем графики имеют ограничения: график не может включить столько данных, сколько входит в таблицу, кроме того, на графике показываются всегда округленные данные, приблизительные. Итак, график используется только для изображения общей ситуации, а не деталей.
По способу построения графики делятся на диаграммы, картограммы и картодиаграммы.
Наиболее распространенным способом графического изображения данных являются диаграммы. Вид диаграмм зависит от вида представляемых данных (одна переменная, один показатель, несколько переменных и т.д.) и задачи построения графика.
В любом случае график обязательно сопровождается заголовком - над или под полем графика. В заголовке указывается, какой показатель изображен, в каких единицах измерения, по какой территории и за какое время он определен.
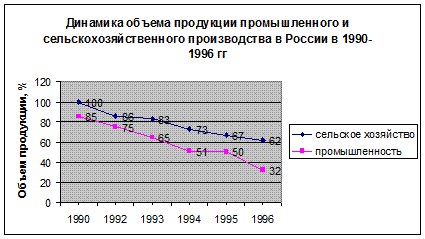
Линейные графики используются для представления количественных переменных: динамика, взаимосвязи между переменными.
Линейные графики разделяют на используемые для представления одной переменной - одномерные или по двум переменным - двумерные, многих переменных - многомерными. Для того, чтобы динамика двух и более переменных показателей была сопоставима, необходимо обеспечить их единое начало. Например, на следующем рисунке изображен график
|
При графическом изображении динамики по оси абсцисс показывается время (годы, кварталы, месяцы); по оси ординат - значения показателя или показателей. При этом ось ординат должна иметь начало в точке "нуль".
Иногда при больших изменениях прибегают к логарифмической шкале. Предположим, значения показателя изменяются от 1 до 100 в (100 раз); это может вызвать затруднения при построении графика. Если перейти к логарифмам, то их значения будут различаться не так сильно: log 1 = 0, log 100 = 2.
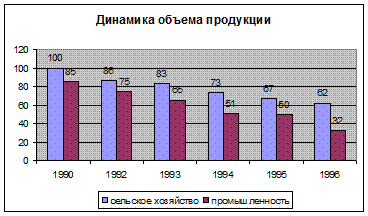
Среди плоскостных диаграмм по частоте использования выделяются столбиковые диаграммы, на которых показатель представляется в виде столбика, высота которого соответствует значению показателя.
Примером может служить следующая диаграмма:
|
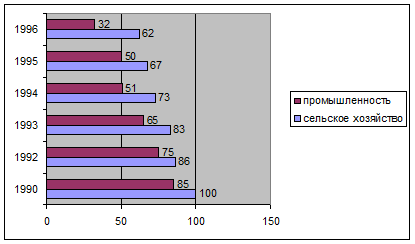
Ленточная диаграмма представляет показатели в виде горизонтально вытянутых прямоугольников. Как столбиковые, так и ленточные диаграммы можно применять не только для сравнения самих величин, но и для сравнения их частей.
Пример ленточной диаграммы:
|
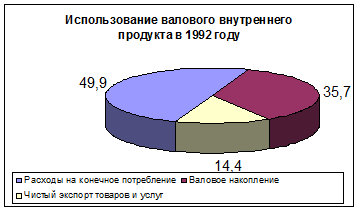
Из плоскостных диаграмм часто используют секторную диаграмму. Она применяется для иллюстрации структуры изучаемой совокупности. Вся совокупность принимается за 100%, ей соответствует общая площадь круга, площади секторов соответствуют частям совокупности. Примером может служить следующая диаграмма.
|
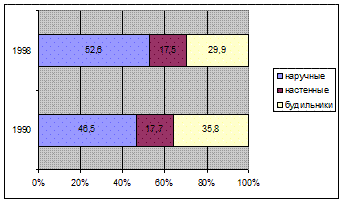
В качестве графического образа для изображения структуры могут быть применены и прямоугольники. Чтобы построить эту диаграмму абсолютные величины необходимо заменить относительными. В этом случае каждая полоса диаграммы будет иметь одинаковую длину. Графическое изображение структуры с помощью столбиков (полос) позволяет изучить особенности многих изучаемых явлений. Например, следующие данные, приведенные в таблице можно изобразить следующим образом:
Производство часов по видам в одном из регионов России за 1990 - 1998г.
| Млн. шт. | % | Млн. шт. | % | |
| Наручные | 24; | 46,5 | 31,6 | 52,6 |
| Настенные | 9,3 | 17,7 | 10,5 | 17.5 |
| Будильники | 18,8 | 35,8 | 18,0 | 29,9 |
Здесь от абсолютных величин мы перешли к % (3 и 4 графа) и получаем следующую диаграмму
|
Дата добавления: 2015-03-03; просмотров: 5610;