Для эффективного применения кэш-памяти рекомендуется использовать многомерные массивы в одномерном виде.
Например, используем
for (i=0; i<m; i++)
{
a[i] = 0.0;
for (j=0; j<n; j++)
a[i] += b[i*n+j]*c[j];
}
Вместо классического
for (i=0; i<m; i++)
{
a[i] = 0.0;
for (j=0; j<n; j++)
a[i] += b[i,j]*c[j];
}
Вложенные циклы следует модифицировать так, чтобы обеспечить последовательный быстрый доступ к элементам массива без скачков по индексам (описано в [1]).
Очень часто загрузку кэш-памяти можно улучшить с помощью транспонирования элементов массивов в петлях вложенных циклов(подробно описано в [4]).
The example code used is a matrix multiplication. We use two square matrices of 1000×1000 double elements. For those who have forgotten the math, given two matrices A and B with elements aij and bij with 0 ≤ i,j < N the product is
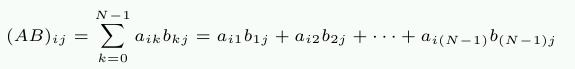
A straight-forward C implementation of this can look like this:
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
for (k = 0; k < N; ++k)
res[i][j] += mul1[i][k] * mul2[k][j];
The two input matrices are mul1 and mul2. The result matrix res is assumed to be initialized to all zeroes. It is a nice and simple implementation.
While mul1 is accessed sequentially, the inner loop advances the row number of mul2. That means that mul1 is handled like the left matrix in Figure 2.7.1 while mul2 is handled like the right matrix. This cannot be good.
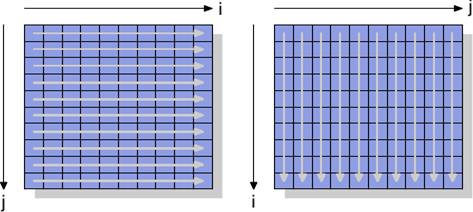
Figure 2.7.1: Matrix Access Pattern
There is one possible remedy one can easily try. Since each element in the matrices is accessed multiple times it might be worthwhile to rearrange (“transpose,” in mathematical terms) the second matrix mul2 before using it.
Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы.
Формально, транспонированная матрица для матрицы A размеров 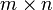 — матрица AT размеров
— матрица AT размеров 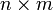 , определённая как AT[i, j] = A[j, i].
, определённая как AT[i, j] = A[j, i].
Например,
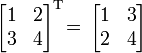 и
и 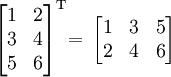
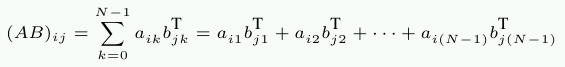
After the transposition (traditionally indicated by a superscript ‘T’) we now iterate over both matrices sequentially. As far as the C code is concerned, it now looks like this:
double tmp[N][N];
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
tmp[i][j] = mul2[j][i];
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
for (k = 0; k < N; ++k)
res[i][j] += mul1[i][k] * tmp[j][k];
We create a temporary variable to contain the transposed matrix. This requires touching more memory, but this cost is, hopefully, recovered since the 1000 non-sequential accesses per column are more expensive (at least on modern hardware). Time for some performance tests. The results on a Intel Core 2 with 2666MHz clock speed are (in clock cycles):
| Original | Transposed | |
| Cycles | 16,765,297,870 | 3,922,373,010 |
| Relative | 100% | 23.4% |
Through the simple transformation of the matrix we can achieve a 76.6% speed-up! The copy operation is more than made up. The 1000 non-sequential accesses really hurt.
На компьютерах серии NUMALINK (non-uniform memory access) с неоднородным по времени доступом к памяти важно учитывать следующие особенности:
- надо хорошо представлять, где запущены потоки;
- надо четко понимать, какие данные загружены в локальную память;
- необходимо знать стоимость доступа к удаленной памяти. Для систем с NUMALINK все вышеперечисленные особенности очень сильно зависят от их архитектуры.
В программах, написанных с использованием OpenMP, существуют следующие возможности управления потоками:
- можно запускать поток на определенном процессоре;
- можно размещать данные в определенном месте памяти.
Эти задачи решаются с помощью системных инструкций, которые могут быть различными на различных платформах и зависеть от используемого системного программного обеспечения.
Дата добавления: 2015-02-03; просмотров: 1182;
