Алгоритм применения критерия Михайлова.

1. Получаем передаточную функцию системы.

2. Составляем характеристическое уравнение системы (это знаменатель передаточной функции).

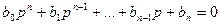
3. В характеристическом уравнении заменяем р на jw.

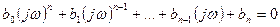
4. Выделяем действительную и мнимую часть.

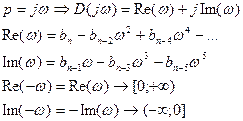
Действительная часть характеристического уравнения является функцией четной, а мнимая часть – нечетной. Поэтому достаточно ограничиться построением кривой, соответствующей характеристическому полиному для положительных частот. Тогда кривая, соответствующая отрицательным частотам является зеркальным отражением кривой для положительных частот относительно оси абсцисс.

5. Изменяем частоту 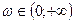и для каждой частоты строим точку на комплексной плоскости, и соответствующий годограф характеристического уравнения.

6. Судим об устойчивости системы по критерию Михайлова.

Если годограф начинается и заканчивается на действительной оси, то система будет устойчивой, в противном случае – наоборот.