Критерий Рауса

САУ будет устойчивой, если будут положительны все элементы первого столбца матрицы Рауса (включая а₀ и а₁).

,

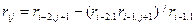где i – номер строки, j – номер столбца.

Если не все коэффициенты столбца положительны, то система неустойчива. При этом число перемен знака среди этих коэффициентов соответствует числу правых корней характеристического уравнения.

Матрица:

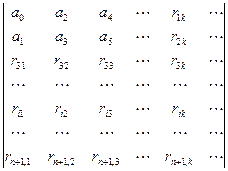
Пример:

Характеристическое уравнение: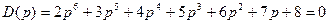

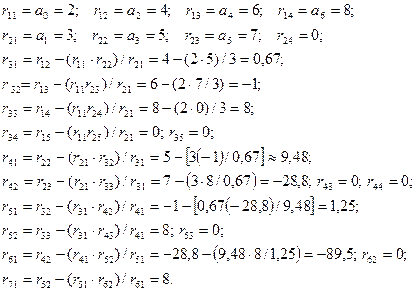
Алгебраические критерии устойчивости для систем выше пятого порядка становятся трудоемкими для вычисления. Кроме того, алгебраические критерии не отражаются наглядностью, поэтому на практике широкое распространение получили частотные критерии устойчивости: критерий Михайлова, критерий Найквиста. И тот, и другой критерии базируются на принципе комплексного аргумента.