Понятие устойчивости по Ляпунову.

Пусть САУ описывается с помощью системы уравнений при заданных начальных условиях:

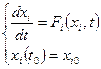
Решением данного уравнения является 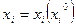как функция начальных значений (уравнение невозмущенного движения). Здесь x_i⁰ – установившееся движение.

К системе приложено внешнее воздействие, которое привело к отклонению движения от установившегося

.

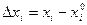Для данных отклонений можно записать систему уравнений:

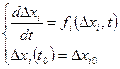
Уравнение 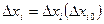- является уравнением возмущенного движения.

Невозмущенное движение ( 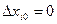) называется устойчивым по отношению к переменным x_i, если для любого положительного числа А², как бы мало оно ни было, найдется другое положительное число l², которое удовлетворяет условию для всех возмущений:

,

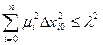а возмущенное движение удовлетворяет условию

,

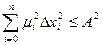где m_i – весовые коэффициенты.

Движение будет устойчивым, если при небольших изменениях начальных условий, вызванных внешними воздействиями, невозмущенное движение будет отличаться от возмущенного движения мало.

Данное определение справедливо как для линейных, так и для нелинейных систем.

Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением

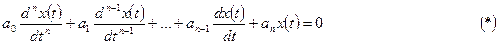
где 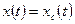- свободная составляющая выходной величины системы.

Система является устойчивой, если свободная составляющая x_c(t) переходного процесса с течением времени стремится к нулю, т.е. если

.

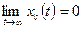Такая устойчивость называется асимптотической.