Формулировка критерия Михайлова.
Автоматическая система управления, описываемая уравнениями п-го порядка будет устойчивой, если при изменении частоты от 0 до ¥ характеристический вектор системы (годограф Михайлова) повернется против часовой стрелки на угол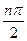 
, не обращаясь при этом в нуль.
 |
Это означает, что характеристическая кривая устойчивой системы должна при изменении w от 0 до ¥ пройти последовательно через п квадрантов.
На рисунке а) изображен вектор D(jw), называемый характеристической кривой или годографом Михайлова. Характеристические кривые, соответствующие устойчивым системам (рисунок б)), имеют плавную спиралеобразную форму и уходят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадрантов не последовательно или проходит меньшее число квадрантов, то система неустойчива (рисунок в)).
В практических расчетах удобно применять следствие из критерия Михайлова:
Система устойчива, если действительная и мнимая части характеристической функции D(jw) обращаются в нуль поочередно (см. рисунок г)), т.е. если корни уравнений Re(w)=0 и Im(w)=0 перемежаются.
Критерий Михайлова удобно применять для анализа устойчивости систем высокого порядка (n>5).
Дата добавления: 2015-02-16; просмотров: 945;