Выбор критерия оценки качества модели

Различные алгоритмы порождают необходимость определиться с множеством различных критериев. В частности, необходимо выбрать критерий включения переменных в модель и их исключения, критерий останова алгоритма и критерий оценки окончательной модели.

Общий принцип останова шаговых алгоритмов структурной идентификации следующий: расчеты надо прекращать, когда дальнейшая работа алгоритма не приводит к улучшению качества модели. Отсюда следует общность критериев останова и качества модели.

Критерий оценки качества модели зависит от ее назначения. Например, если предполагается использовать модель для управления или прогнозирования, то необходима высокая прогностическая способность модели — на одни и те же входные воздействия модель и объект должны давать близкие результаты на выходе. Если модель используется в системе измерений, то целью является минимум максимального отклонения значений модели и объекта. Если необходимо построить распознающую систему, то в качестве критерия берут ошибку распознавания — отношение правильных ответов к общему их числу.

Если ограничиться задачей управления, то в основу искомого критерия останова можно заложить требование близости значений выхода модели у^м и объекта у при одинаковых значениях входных переменных 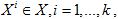где Х – рабочая область изменения входных переменных:

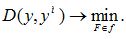
Наиболее распространен следующий критерий оценки качества модели:

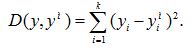
В приведенном виде среднеквадратичная ошибка отклонения рассчитывается в процентах от среднего значения

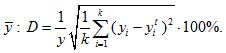
Все критерии останова, алгоритмов структурной идентификации (они же критерии качества модели), за исключением критерия достижения заданного числа входных переменных в модели и ему подобных, можно разбить на две группы: внутренние и внешние. Внутренние критерии вычисляются на основании данных, участвующих в построении модели, а внешние — на основании дополнительных данных.

К внутренним критериям, в первую очередь, следует отнести остаточную ошибку модели — сумму отклонений (абсолютных или квадратов разностей) значений выходных переменных объекта и модели. Далее следует назвать коэффициент детерминации (квадрат множественного коэффициента корреляции R²), приведенную остаточную ошибку, приведенный R² и критерий Марллоуса С_р, а также другие критерии.

Более надежным представляется использование нескольких выборок данных: по одним выборкам строится модель, а по другим — оценивается ее качество.

В ряде работ дополнительные экспериментальные данные (экзаменационные точки) предлагается применять для оценки качества готовых моделей. Таким образом, предлагается из множества экспериментальных данных выделять часть точек в качестве контрольных. Среднеквадратичная ошибка на этих точках может служить в качестве критерия останова алгоритмов структурной идентификации.

Если наблюдать поведение модели на дополнительных экспериментальных точках, то можно заметить, что, начиная с некоторого шага, модель начинает удаляться от этих точек (в случае неустойчивости это удаление начинается с первого же шага). Исходя из этого, предлагается определять момент останова алгоритма по ошибке на контрольных точках - расчеты прекращаются в момент достижения первого минимума ошибки по шагам алгоритма.

В силу независимости от конкретного алгоритма, в качестве критерия качества готовых моделей или для сравнения моделей, построенных с помощью различных алгоритмов, предлагается также использовать среднеквадратичную ошибку на контрольных точках.