Оценивание параметров модели

Будем считать, что нам известна структура модели (оператора F), но не известны коэффициенты (параметры) этой модели. Какой бы точной ни была структура модели, практически всегда имеются параметры, которые необходимо найти или уточнить. Задача оценивания параметров модели ставится как задача оптимизации: необходимо найти такой вектор параметров А из области допустимых значений Ω, чтобы минимизировать некоторую функцию отклонения значений выхода модели (у^м) от выхода объекта (у) при одних и тех же значениях входных переменных:

Пример. Пусть известна структура модели: у^м=а₀ + а₁х. Необходимо по k измерениям y и x найти параметры модели а₀ и а_{1 .} Запишем критерий:

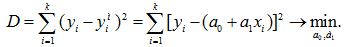
Для нахождения а₀ и а₁, приводящих к минимизации заданный критерий D, возьмем частные производные от D по а₀ и а₁ и приравняем их нулю (из математики известно, что в точках экстремума функции ее производная равна нулю):

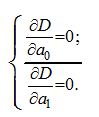
В результате получается система двух линейных уравнений с двумя неизвестными, решение которой и дает искомые значения параметров а₀ и а₁:

Однако для применения этого метода предъявляются определенные требования к данным:

а) входные переменные модели должны быть линейно независимые, что выполняется;

б) помехи, действующие на систему, должны иметь нормальное распределение.

Эти требования выполняются далеко не всегда, что может привести к ненадежным оценкам параметров модели. Другой проблемой является ограниченность имеющейся выборки данных (набор экспериментальных точек). Для параметров модели используется эмпирическое правило: для корректной, надежной оценки одного параметра необходимо 5-10 экспериментальных точек. Однако бывают ситуации, когда получение достаточного числа точек крайне затруднено или очень дорого.

2.2.3 Математическое моделирование

Математическое моделирование - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ.

Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.

В общем случае математическая модель реального объекта, процесса или системы представляется в виде системы функционалов:

Ф_i ( X , Y , Z , t )=0,

где X - вектор входных переменных, X =[ x₁ , x₂ , x₃ , ... , x_N ] t ,

Y - вектор выходных переменных, Y =[ y₁, y₂, y₃, ... , y_N ] t ,

Z - вектор внешних воздействий, Z =[ z₁, z₂, z3, ... , z_N ] t ,

t - координата времени.

Построение математической модели заключается в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат [5].

При построении математической модели перед исследованием возникает задача выявить и исключить из рассмотрения факторы, несущественно влияющие на конечный результат (математическая модель обычно включает значительно меньшее число факторов, чем в реальной действительности). На основе данных эксперимента выдвигаются гипотезы о связи между величинами, выражающими конечный результат, и факторами, введенными в математическую модель. Такая связь зачастую выражается системами дифференциальных уравнений в частных производных (например, в задачах механики твердого тела, жидкости и газа, теории фильтрации, теплопроводности, теории электростатического и электродинамического полей).

Конечной целью этого этапа является формулирование математической задачи, решение которой с необходимой точностью выражает результаты, интересующие специалиста.

По принципам построения математические модели разделяют на :

• аналитические;

• имитационные.

В аналитических моделях процессы функционирования реальных объектов, процессов или систем записываются в виде явных функциональных зависимостей.

Аналитическая модель разделяется на типы в зависимости от математической проблемы:

• уравнения (алгебраические, трансцендентные, дифференциальные, интегральные),

• аппроксимационные задачи (интерполяция, экстраполяция, численное интегрирование и дифференцирование),

• задачи оптимизации,

• стохастические проблемы.

Однако по мере усложнения объекта моделирования построение аналитической модели превращается в трудноразрешимую проблему. Тогда исследователь вынужден использовать имитационное моделирование.

В имитационном моделировании функционирование объектов, процессов или систем описывается набором алгоритмов. Алгоритмы имитируют реальные элементарные явления, составляющие процесс или систему с сохранением их логической структуры и последовательности протекания во времени. Имитационное моделирование позволяет по исходным данным получить сведения о состояниях процесса или системы в определенные моменты времени, однако прогнозирование поведения объектов, процессов или систем здесь затруднительно. Можно сказать, что имитационные модели - это проводимые на ЭВМ вычислительные эксперименты с математическими моделями, имитирующими поведение реальных объектов, процессов или систем.

В зависимости от характера исследуемых реальных процессов и систем математические модели могут быть:

• детерминированные,

• стохастические.

В детерминированных моделях предполагается отсутствие различных случайных воздействий, элементы модели (переменные, математические связи) достаточно точно установленные, поведение системы можно точно определить. При построении детерминированных моделей чаще всего используются алгебраические уравнения, интегральные уравнения, матричная алгебра.

Стохастическая модель учитывает случайный характер процессов в исследуемых объектах и системах, который описывается методами теории вероятности и математической статистики.

По степени соответствия между математической моделью и реальным объектом, процессом или системой математические модели разделяют на :

• изоморфные (одинаковые по форме),

• гомоморфные (разные по форме).

Модель называется изоморфной, если между нею и реальным объектом, процессом или системой существует полное поэлементное соответствие. Гомоморфной - если существует соответствие лишь между наиболее значительными составными частями объекта и модели.

Контрольные вопросы к разделу:

1. Дайте определение понятия «модель», «моделирование»

2. Какие принципы моделирования существуют?

3. Для каких целей создаются дескриптивные модели?

4. Какие существуют особенности моделей по сравнению с реальными объектами?

5. Дайте определение системного анализа. Какие основные этапы включает системный анализ?

6. Перечислите подходы к анализу и проектированию систем.

7. Какие общие этапы можно выделить в методологии системного анализа?

8. Что такое система и из чего она состоит?

9. Существует ли в природе системы как таковые?

10. Какие основные признаки используется для классификации систем?

11. Какими свойствами характеризуются системы? Какие принципы для них характерны?

12. В чем состоит принципиальные отличия между сложными и простыми системами?

13. Какой (гомогенной или гетерогенной) системой является фабрика?

14. Охарактеризуйте статистические и динамические системы. Приведите примеры.

15. Какое содержание имеет термин «эмерджентность»?

16. Чем отличаются статистические и динамические системы?

17. Перечислите основные принципы системного анализа.

Список использованной литературы

1. Анфилатов B.C., Емельянов А.А.. Кукушкин А.А. Системный анализ в управлении. - М.: Финансы и статистика, 2003. - 368 с.

2. Волкова В.Н. Концепции современного естествознания: Учебное пособие. - СПб.: Изд-во Политехи, ун-та, 2006. - 200 с.

3. Волкова В.Н., Денисов А.А. Основы теории управления и системного анализа. - СПб.: Изд-во СПбГТУ, 1997. - 510 с.

4. Качала В.В. Основы теории систем и системного анализа. Учебное пособие для вузов. М.: Горячая линия – Телеком, 2007. 216 с.

5. О'Конор Д., Мак-Дермот Я. Искусство системного мышлении. Творческий подход к решению проблем и его основные стратегии. Киев: София, 2001. - 304 с.

6. Прангишвили И.В. Системный подход и общесистемные закономерномерности - М.: СИН-ТЕГ, 2000. - 528 с.

7. Системный анализ и принятие решений: Словарь-справочник: Учебное пособие для вузов / Под ред. В.Н. Волковой. В. Н. Козлова. - М.: Высш. шк. 2004. - 616 с.

8. Сурмин Ю.П. Теория систем и системный анализ: Учеб. пособие.- Киев: МЛУП, 2003. - 368 с.