Общесистемные закономерности
| 1. Закономер-ности взаимо-действия части и целого | 1.1 Эмерджент-ность (или интеграти-вность) | Эмерджентность (от англ. emergence — возникновение, явление нового) — это возникновение в системе новых интегративных качеств, не свойственных ее компонентам в отдельности. Эмерджентность является одной из форм проявления диалектического закона перехода количественных изменений в качественные. Чем проще система, чем из меньшего числа элементов и связей она состоит, тем меньше проявляет она системное качество, и чем сложнее система, тем более непохожим является ее системный эффект по сравнению со свойствами каждого элемента. Из данной закономерности следует важный практический вывод: невозможно предсказать свойства системы в целом, разбирая и анализируя ее по частям. |
| 1.2. Целост-ность. | Изменение в одном элементе системы вызывает изменения во всех других элементах и в системе в целом. Целостность возникает благодаря связям в системе, которые осуществляют перенос свойств каждого элемента системы ко всем остальным элементам. Предельным случаем целостности является абсолютная целостная система. Благодаря абсолютно жестким связям такая система может находиться только в одном состоянии, поэтому энтропия ее равна нулю. В реальных системах связи между элементами не являются абсолютно жесткими (к < 1), из-за чего система может находиться в нескольких состояниях. В этом случае воздействие на элемент системы отразится во всех элементах и в системе в целом, но с неким «затуханием». | |
| 1.3 Синергизм | Проявляется в виде мультипликативного эффекта при однонаправленных действиях. Примеры: если система имеет два входа (х1 и х2)и один выход у, тогда мультипликативный эффект можно выразить уравнением у = ax1x2. Пример: В медицине часто можно наблюдать явление, когда комбинированное действие лекарственных веществ на организм превышает действие, оказываемое каждым компонентом в отдельности. В экономике доходы от совместного использования ресурсов превышают сумму доходов от использования тех же ресурсов по отдельности. | |
| 2. Законно-мерности иерархи-ческой упорядо-ченности систем | 2.1 Коммуника- тивность | Любая система не изолирована от других систем, но связана множеством коммуникаций с окружающей средой, которая представляет собой сложное и неоднородное образование, содержащее: - надсистему (систему более высокого порядка, задающую требования и ограничения рассматриваемой системе); - элементы или подсистемы (нижележащие, подведомственные системы); - системы одного уровня с рассматриваемой. В силу закономерности коммуникативности каждый уровень иерархической упорядоченности имеет сложные взаимоотношения с вышестоящим и нижележащим уровнями. |
| 2.2 Иерархич-ность | Любую систему можно представить в виде иерархического образования. При, этом на всех уровнях иерархии действует закономерность целостности. Более высокий иерархический уровень объединяет элементы нижестоящего и оказывает на них направляющее воздействие. | |
| 3. Энтро-пийные законно-мерности | 3.1 Принцип компенсации энтропии | Что энтропия неизолированной системы может быть уменьшена только за счет компенсирующего увеличения энтропии в другой или других системах взаимодействующих с данной. На основе вышеизложенного, можно утверждать, что прогресс не может быть общим для всех частей системы. По законам термодинамики снижение энтропии в одной части системы обязательно сопровождается повышением энтропии в другой части или окружающей среде. |
| 4. Законно-мерности развития | 4.1.Закон-омерность развития во времени – историч-ность | Любая система не может быть неизменной, что она не только возникает, функционирует, развивается, но и погибает — любая система имеет свой жизненный цикл. |
| 4.2 Рост и развитие | Развитие - это изменения процессов в системе во времени, выраженные в количественных, качественных и структурных преобразованиях от низшего (простого) к высшему (сложному). Деградация - постепенное ухудшение, снижение или утрата положительных качеств, упадок, | |
| 4.3 Закономер-ность неравномер-ного развития и рассогласо-вания темпов выполнения функций элементами системы | Чем сложнее система, том более неравномерно развиваются ее составные части. При этом в процессе функционирования или развития системы ее элементы выполняют свои локальные функции в соответствии со своим темпом. Это закономерно приводит к рассогласованию темпов выполнения функций элементами, что создает угрозу целостности системы и ее способности выполнять свои функции, а также дезорганизации всей системы вплоть до ее остановки. | |
| 4.4 Эквифиналь-ность | Состояние равновесия в закрытых системах полностью определяется начальными условиями. Для открытых же систем их конечное состояние не зависит от начального состояния, а определяется особенностями протекающих внутри системы процессов и характером ее взаимодействия со средой. Эквифинальность - это способность системы достигать определенного состояния, которое не зависит ни от времени, ни от ее начальных условий, а определяется исключительно ее параметрами. | |
| 5.Другие общесис-темные законно-мерности | 5.1 Полисистем-ность | Любой объект окружающего мира принадлежит в качестве элемента одновременно многим системам. При этом между всеми системами, которым принадлежит общий элемент, существуют противоречия: каждая из этих систем стремится к своей, особой цели, используя любой свой элемент в качестве средства. |
| 5.2Противо-действие системы внешнему возмущению | А.Л. Ле Шателье сформулировал следующий принцип: «Если существующее равновесие системы подвергается внешнему воздействию, изменяющему какое-либо из условий равновесия, то в ней возникают процессы, направленные так, чтобы противодействовать этому изменению», т.е. при внешнем возмущении, нарушающем условие равновесия, в системе развиваются противоположно действующие процессы, и до определенного уровня они нейтрализуют эффект внешнего воздействия. | |
| 5.3 Закономер-ность «наиболее слабых мест» | Устойчивость всей системы зависит от наиболее слабых элементов в системе, поэтому структурная устойчивость (приспособленность) системы определяется устойчивостью наиболее слабой подсистемы. Там, где относительное сопротивление будет меньше необходимого, произойдет сбой. |
2.1.4 Характеристики системы.
Одной из наиболее важных задач системного анализа является установление причинно-следственных связей выходов системы с ее входами и состоянием. Значения выходов системы зависят от следующих факторов:
- значений входных переменных;
- начального состояния системы;
- функции системы.
1. Состояние системы и его оценка
Состояние системы характеризует ее свойства в определенный момент времени. При этом можно говорить о состоянии входов, внутреннем состоянии и состоянии выходов системы.
Состояние входов системы представляется вектором значений входных параметров X = (x1,...,xn) и фактически является отражением состояния окружающей среды.
Внутреннее состояние системы представляется вектором значений ее внутренних параметров (параметров состояния): Z = (z1,...,zv) и зависит от состояния входов Х и начального состояния Z0:
Z = F1(X,Z0).
Примерами параметров состояния служат температура газа в трубе, психологическое состояние человека, степень изношенности оборудования, уровень квалификации персонала.
Внутреннее состояние практически ненаблюдаемо, но может быть оценено по состоянию выходных переменных системы Y = (y1...ym) благодаря зависимости Y= F2(Z).
При этом в качестве характеристик, отражающих состояние системы, могут выступать не только сами выходные значения, но и характеристики их изменения - скорость, ускорение и т. д. Таким образом, внутреннее состояние системы S в момент времени t может характеризоваться множеством значений ее выходных координат и их производных в этот момент времени:
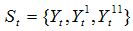
Например, состояние финансовой системы страны можно характеризовать не только курсом национальной валюты к доллару, но и скоростью изменения этого курса, а также ускорением или замедлением этой скорости.
При этом выходные переменные могут не полностью, неоднозначно и несвоевременно отражать состояние системы в данный момент времени.
Если у больного повышенная температура {у > 37 °С), то это может быть характерно для различных внутренних состояний. Или если у предприятия низкая прибыль, то это может быть при разных состояниях организации
2. Процесс
Если система способна переходить из одного состояния в другое (например, S1→S2→S3...), то говорят, что она обладает поведением - в ней происходит процесс (Р), который может быть описан через функцию времени: P=S(t), или множеством: P = {St1 St2….},
По отношению к системе существует два вида процессов:
- внешний процесс - последовательная смена воздействий на систему, (последовательная смена состояний внешней среды);
- внутренний процесс - последовательная смена состояний системы, которая наблюдается как процесс на выходе системы.
3. Изменение системы
В зависимости от того, изменяется ли состояние системы со временем, ее можно отнести к статическим пли динамическим системам.
Статические модели отражают функцию системы - конкретное состояние реальной или проектируемой системы (например, закон Ома). Динамические модели отражают процесс функционирования или изменения состояний системы (различия между состояниями, последовательность смены состояний и развитие событий с течением времени).
Например, описание процесса изменения спроса на какой-либо товар под влиянием рекламы, изменение температуры утюга при его включении.
Отличие статических и динамических моделей заключено в учете времени: в статике его как бы не существует, а в динамике оно является основным элементом.
Для описаний функционирования системы используются динамические модели.
Для разных объектов и систем разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, до формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля.
4. Функция и функционирование системы
Свойства системы проявляются не только в значениях выходных переменных, но и в ее функциях, поэтому определение функций системы является одной из первых задач ее анализа или проектирования.
Функция системы — это способ (правило, алгоритм) преобразование входной информации в выходную.
Система может быть одно- или многофункциональной.
Функцию динамической системы можно представить логико-математической моделью, связывающей входные (X) и выходные (Y) координаты системы: Y = F(Х),
где F - оператор (в частном случае некоторая формула), называемый алгоритмом функционирования, — вся совокупность математических и логических действий, которые нужно произвести, чтобы по данным входам Х найти соответствующие выходы Y.
Функционирование рассматривается как процесс реализации системой своих функций и описывает, как меняется состояние системы при изменении состояния ее входов.
5. Состояние функции системы
Поскольку функция системы является ее свойством, то можно говорить о состоянии системы в заданный момент времени, указывая ее функцию для этого момента времени. Таким образом, состояние системы можно рассматривать в двух разрезах: состояние ее параметров и состояние ее функции, которая, в свою очередь, зависит от состояния структуры и параметров: St = {At,Ft} = {At,(St,At)}
Знание состояния функции системы позволяет прогнозировать значения ее выходных переменных для стационарных систем.
Систему считают стационарной, если ее функция практически не изменяется в течение определенного периода ее существования. Для такой системы реакция на одно и то же воздействие не зависит от момента приложения этого воздействия.
Ситуация значительно осложняется, если функция системы меняется во времени, что является свойством нестационарных систем. Систему считают нестационарной, если ее функция изменяется со временем.
6. Режимы динамической системы
Динамическая система может находиться в трех режимах: равновесный, переходной и периодический.
Равновесный режим — это такое состояние системы, в котором она может находиться сколь угодно долго в отсутствие внешних возмущающих воздействий или при постоянных воздействиях.
Под переходным режимом понимают процесс движения динамической системы из некоторого начального состояния к какому-либо ее установившемуся режиму - равновесному или периодическому.
Периодическим режимом называется такой режим, когда система через равные промежутки времени приходит в одни и те же состояния [5,7,8].
2.1.5. Понятие системного анализа
Под системным анализом понимают одно из направлений системного подхода к изучению больших и/или сложных систем, предполагающее мысленное расчленение сложного (целого) объекта для выявления его наиболее существенных частей - компонентов и свойств .
Системный подход – это направление методологии научного познания и социальной практики, в основе которого лежит рассмотрение объектов как системы. Системный подход ориентирует исследователей на раскрытие целостности объекта, на выявление многообразных связей и сведение их в единую теоретическую картину.
Системный синтез - направление системного подхода, концертирующее внимание на органическом соединении различных частей рассматриваемого сложного объекта в единое, целостное образование, уже обладающего качественно новыми свойствами, включая и способность к самоорганизации путем усложнения и дифференциации.
Дата добавления: 2015-01-24; просмотров: 3096;
