Методы и алгоритмы выбора структур моделей.

Методы шаговой регрессии. Основная идея шаговой (пошаговой) регрессии заключается в гипотезе о том, что искомую структуру можно найти, трансформируя модель путем следующих последовательных действий:

1) добавления к модели наиболее значимых по некоторому критерию переменных (метод включения, или «присоединения»);

2) исключения незначимых по некоторому критерию переменных (метод исключения, или «удаления»);

3) добавления наиболее значимых переменных при одновременном исключении незначимых (метод добавления-исключения, или «присоединения-удаления»).

В качестве добавляемых (удаляемых) переменных могут выступать не только сами исходные переменные x₁, …, x_m, но и функции от них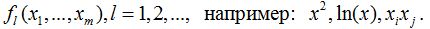

Частным случаем функций можно считать и функции вида: 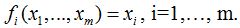Таким образом, с помощью шаговой регрессии можно строить нелинейные (нелинейные по переменным, но линейные по параметрам) математические модели вида

y = a₀ +∑ a_if_i(x₁…..x_m).

Метод включения начинает свою работу с выбора наиболее значимой (по некоторому критерию) переменной (функции) из списка: 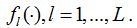Затем из оставшихся переменных выбирается наиболее значимая и включается в модель. И так до тех пор, пока улучшается качество модели. Качество последней во многом зависит от порядка вхождения переменных в модель, который, в свою очередь, определяется используемым критерием включения. Поскольку между переменными практически всегда имеется ненулевая корреляционная зависимость, то не выполняется правило аддитивности. В результате переменная, значимая на предыдущих шагах, может стать незначимой на последующих, и ее присутствие может препятствовать включению в модель другой, более значимой переменной. Эта особенность ограничивает возможность метода включения.

Метод исключения первоначально рассматривает модель, в которую включены все имеющиеся L входных переменных. Затем из них последовательно исключаются незначимые (по некоторому критерию) переменные до тех пор, пока улучшается качество модели. Структура конечной модели может совпадать со структурой, полученной по методу включения, но для сложных моделей это скорее исключение, чем правило. Данному методу присущ недостаток метода включения: исключенные на предыдущих шагах переменные могут оказаться значимыми после исключения других переменных. Кроме того, к недостаткам можно отнести и повышенные требования к вычислительным ресурсам при работе с массивами большого размера на первых шагах алгоритма, а при небольших выборках экспериментальных данных — алгоритм может вообще не работать (например, если k < L).

Объединение вышеназванных методов дает метод включения-исключения, в основе которого лежит метод включения, но дополнительно на каждом шаге алгоритма происходит проверка переменных на значимость: незначимые переменные исключаются из модели. При кажущейся эффективности такого подхода метод не дает уверенности в оптимальности найденной структуры. В работе предложен алгоритм, автоматически выбирающий порог исключения переменных, что частично решает проблему выбора соответствующего критерия, но опять же не гарантирует нахождения глобального экстремума.

Метод группового учета аргументов (МГУА). Сложно говорить о МГУА как о конкретном методе, поскольку начиная с 1968 г. разработаны десятки его разновидностей. В МГУА можно выделить два направления: комбинаторные и селективные (еще их называют многорядными) алгоритмы.
В комбинаторном алгоритме сначала рассматривается множество моделей от одной переменной:

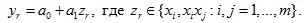
Затем рассматривается множество всех возможных моделей от двух переменных:

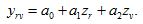
Далее от трех и так до тех пор, пока улучшается критерий D. Возможности комбинаторного алгоритма ограничены возможностями вычислительной техники, поскольку ввод одной дополнительной входной переменной увеличивает время счета примерно вдвое [1,2,7,8].