МНОГОМЕРНЫЕ ГРУППИРОВКИ
Мы убедились, как трудно выбрать какой-то один признак в качестве основания группировки. Еще труднее проводить группировку по нескольким признакам. Комбинация двух признаков позволяет сохранить обозримость таблицы, но комбинация трех или четырех признаков дает совершенно неудовлетворительный результат: ведь даже при выделении трех категорий по каждому из груп-пировочных признаков мы получим 9 или 12 подгрупп. Равномерность распределения единиц по группам в принципе невозможна. Вот и получаются группы, в которые входят 1-2 наблюдения. Сохранить сложность описания групп и вместе с тем преодолеть недостатки комбинационной группировки позволяютметоды многомерных группировок. Часто их называютметодами многомерной классификации.
Эти методы получили распространение благодаря использованию |ЭВМ и пакетов прикладных программ. Цель этих методов — классификация данных, иначе говоря, группировка на основе множества |Признаков. Такие задачи широко распространены в науках о приро-|де и обществе, в практической деятельности по управлению массо-^Яыми процессами. Например, выделение типов предприятий по Ижнансовому положению, по экономической эффективности деятельности производится на основе множества признаков: выделение и изучение типов людей по степени их пригодности к определенной профессии (профпригодность); диагностика болезней на основании множества объективных признаков (симптомов) и т. д.
Простейшим вариантом многомерной классификации является группировка на основе многомерных средних.
Многомерной средней называется средняя величина нескольких признаков для одной единицы совокупности. Поскольку нельзя рассчитать среднюю величину абсолютных значений разных признаков выраженных в разных единицах измерения, то многомерная средняя вычисляется из относительных величин, как правило, - из отношений значений признаков для единицы совокупности к средним значениям этих признаков:
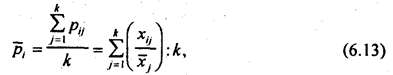
где p̅j - многомерная средняя для i-единицы;
хij - значение признака х, для г-единицы;
хj - среднее значение признака xi,
k - число признаков;
j - номер признака;
i - номер единицы совокупности.
Рассмотрим использование многомерных средних на примере сельскохозяйственных предприятий Всеволожского района Ленинградской области за 1995 г. (табл. 6.8). По каждому предприятию приведены четыре признака:
• среднемесячная оплата труда работника, руб., x1;
• валовой доход на 1 га сельхозугодий, тыс. руб./га, х2;
• среднегодовая стоимость основных производственных фондов на 1 га сельхозугодий, млн руб./га, x3;
• отношение дебиторской задолженности к кредиторской задолженности, %, x4.
Эти признаки можно считать однородными, так как большая их величина положительно характеризует экономику предприятия. Предпочтительнее обобщать в многомерной средней признаки либо «положительные», либо «отрицательные» (чем больше, тем хуже).
Многомерные средние, приведенные в последней графе табл. 6.8, обобщают четыре признака.. При этом значимость признаков для оценки предприятия полагается одинаковой, что, конечно, спорно. Можно .усложнить методику, приписав признакам, на основе экспертнои оценки, разные веса, и вычислить взвешенные многомерные средние.
Таблица 6.8
Дата добавления: 2015-01-21; просмотров: 1112;
